trac_ik

误差阀值eps。来自TRAC_IKKinematicsPlugin::searchPositionIK(...)栈内变量“double epsilon = 1e-5”，是个不能改的参数。
逆解溢出时间maxtime，单位秒。来自param：/robot_description_kinematics/robot_arm/kinematics_solver_timeout。中间“robot_arm”是规划组名称。该param定义在文件kinematics.yaml。建议值或许是0.5，即default_ik_timeout_的默认值。
solvetype不是Speed时，trac_ik会用足maxtime，从而求出多个可能的逆解。Speed时，找到一个逆解就结束。
由delta_twist算出的error[0]将用于计算后面导函数误差 $\Delta f$ ，它应该正确、灵敏反应出不同 $q$ 值时的变化。一旦不正确或不灵敏，会影响nlopt的收敛速度，结果造成时间溢出，逆解失败
errors是个std::vector，单元类型std::pair<double, uint>，first是误差，用于“std::sort(errors.begin(), errors.end())”排序，second则是该逆解在solutions的索引。solutions[errors[0].second]则是基于“err”排序后，得到的最优逆解。

trac_ik和Orocos KDL类似，也是一种基于数值解的机器人运动学求解器，但是在算法层面进行了很多改进。具体来说，KDL的收敛算法基于牛顿方法，在存在关节限制的情况下效果不佳，但这在许多机器人平台上很常见。trac_ik同时运行两个IK实现。一个是对KDL基于牛顿的收敛算法的简单扩展，该算法通过随机跳跃检测和减轻由于联合限制引起的局部最小值。第二种是SQP非线性优化方法（Sequential Quadratic Programming，参考“序列二次规划——SQP“），它使用更好地处理关节限制的拟牛顿方法。默认情况下，当两个算法中的任何一个收敛到答案时，IK搜索会立即返回。不论成功率还是计算时间，trac_ik比KDL都要好很多。

编程实现上，trac_ik的两个IK算法独立运行在两个并发线程：TRAC_IK::runKDL和TRAC_IK::runNLOP

class TRAC_IK
{
private:
  // 误差阀值eps。
  // 来自TRAC_IKKinematicsPlugin::searchPositionIK(...)栈内变量“double epsilon = 1e-5”，是个不能改的参数。
  double eps; 
  // 逆解溢出时间maxtime，单位秒。
  double maxtime;
  // 可选{ Speed, Distance, Manip1, Manip2 }，默认使用Speed
  SolveType solvetype;

  std::unique_ptr<NLOPT_IK::NLOPT_IK> nl_solver;
  std::unique_ptr<KDL::ChainIkSolverPos_TL> iksolver;

  // solutions, erros共同存储着逆解出的结果
  std::vector solutions;
  std::vector<std::pair<double, uint> >  errors;
 };

inline bool TRAC_IK::runKDL(const KDL::JntArray &q_init, const KDL::Frame &p_in)
{
  return runSolver(*iksolver.get(), *nl_solver.get(), q_init, p_in);
}

inline bool TRAC_IK::runNLOPT(const KDL::JntArray &q_init, const KDL::Frame &p_in)
{
  return runSolver(*nl_solver.get(), *iksolver.get(), q_init, p_in);
}

NLOPT_IK::NLOPT_IK和KDL::ChainIkSolverPos_TL的构造时机都是在IKConstraintSampler::callIK，即要执行一次把笛卡儿位姿逆解关节状态时。此次逆解一旦结束，它们立即被销毁。

可认为这两线程独立运行，运行中没有需要同步的变量。

一、TRAC_IK::CartToJnt

TRAC_IK::CartToJnt是trac_ik提供的由笛卡儿位姿逆解关节状态的api。

@q_init[IN]：牛顿迭代初值。
@p_in[IN]：要求解的笛卡儿位姿
@q_out[OUT]：存储着逆解出的关节状态
@_bounds[IN]：不是关节范围限制，用于定义位姿误差delta_twist中6个字段的归0阀值。在索引i字段，值“std::abs(delta_twist[i]) <= std::abs(_bounds[i])“时，强制把该误差字段置为0。也就是说，让caller不改eps前提下，有机会可以加大某些分量的允许误差。默认0。

返回值是个整数。小于0表示没找到，大于0表示找到的逆解数。不会出现0。参数@q_out存储着那个最优逆解。

int TRAC_IK::CartToJnt(const KDL::JntArray &q_init, const KDL::Frame &p_in, KDL::JntArray &q_out, const KDL::Twist& _bounds)
{
  ...

  start_time = boost::posix_time::microsec_clock::local_time();

  nl_solver->reset();
  iksolver->reset();

  solutions.clear();
  errors.clear();

  bounds = _bounds;

  task1 = std::thread(&TRAC_IK::runKDL, this, q_init, p_in);
  task2 = std::thread(&TRAC_IK::runNLOPT, this, q_init, p_in);

  task1.join();
  task2.join();

  if (solutions.empty())
  {
    q_out = q_init;
    return -3;
  }

不是Speed类型时，过程中可能找到数个逆解，solutions存储着这些逆解。这里有个问题，最终要返回只是一个逆解，如何判定solutions中哪个逆解最好呢？，——把算出的各逆解减去q_init，求出各分量差的平方和，正如“err = TRAC_IK::JointErr(q_init, q_out)”算出的err。errors中的first就是这个err，second则是该逆解对应的在solutions中的索引。

  switch (solvetype)
  {
  case Manip1:
  case Manip2:
    std::sort(errors.rbegin(), errors.rend()); // rbegin/rend to sort by max
    break;
  default:
    std::sort(errors.begin(), errors.end());

errors类型是std::vector，不是自动排序容器，std::sort执行着把errors按first排序。排序后[0]存储着err最小的逆解，也就是最终要返回的。

    break;
  }

  q_out = solutions[errors[0].second];

经过排序，erros[0]的err最小，erros[0].second指向这个逆解在solutions中索引。

  return solutions.size();
}

二、TRAC_IK::runSolver

两个IK都会执行runSolver，可认为runSolver就是这两个线程的线程函数。

template<typename T1, typename T2>
bool TRAC_IK::runSolver(const std::string& tag, T1& solver, T2& other_solver,
                        const KDL::JntArray &q_init,
                        const KDL::Frame &p_in)
{
  ...
  while (TRUE) {
    ...
    int RC = solver.CartToJnt(seed, p_in, q_out, bounds);

两个IK需要实现自已的CartToJnt(...)，它们的区别全在这个函数。“RC >= 0”表示此次solver.CarToJnt成功得到了一个逆解，存储在变量q_out。

    if (RC >= 0)
    {
      switch (solvetype)
      {
      case Manip1:
      case Manip2:
        normalize_limits(q_init, q_out);
        break;
      default:
        normalize_seed(q_init, q_out);
        break;
      }
      mtx_.lock();
      if (unique_solution(q_out))
      {

不是Speed类型时，一次逆运动学求解可能找到数个逆解。q_out是此轮新找到的逆解，unique_solution(q_out)用于判断这个新逆解值是否是个新值（独一无二，已得出的逆解中不存在），true表示是一个新值。接下，一是把这个新值放入solutions。二是算出可用于比较的该逆解优劣的误差(err)，放入errors。

errors是个std::vector，单元类型std::pair<double, uint>，first是误差，用于“std::sort(errors.begin(), errors.end())”排序，second则是该逆解在solutions的索引。solutions[errors[0].second]则是基于“err”排序后，得到的最优逆解。

两个线程都要执行TRAC_IK::runSolver，它们有可能同时修改共享变量solutions、errors，因而修改它们须要加互斥锁mtx_。

        solutions.push_back(q_out);
        uint curr_size = solutions.size();
        errors.resize(curr_size);
        mtx_.unlock();
        double err, penalty;
        switch (solvetype)
        {
        case Manip1:
          ...
          break;
        case Manip2:
          ...
          break;
        default:
          err = TRAC_IK::JointErr(q_init, q_out);
          break;
        }
        mtx_.lock();
        errors[curr_size - 1] = std::make_pair(err, curr_size - 1);
      }
      mtx_.unlock();
    }

    if (!solutions.empty() && solvetype == Speed) {
      break;

一个IK的solver.CartToJnt(...)找到逆解后，会把逆解放入solutions。当另外一个IK运行到这里，发现solutions非空，就break出while，从而退出自个线程。

    }
    ...
  }
  ...
}

一个IK找到逆解后，如何通知另外一个IK线束线程？——在两个IK都会执行的TRAC_IK::runSolver，一个IK找到逆解后，会把逆解放入TRAC_IK::solutions。当另外一个IK运行检测solutions.empty()，发现非空，就退出线程。

三、TRAC_IK::runKDL

运行着类似KDL的牛顿迭代算法。在runKDL，核心操作是调用ChainIkSolverPos_TL.CartToJnt(...)。

class ChainIkSolverPos_TL
{
public:
  int CartToJnt(const KDL::JntArray& q_init, const KDL::Frame& p_in, KDL::JntArray& q_out, const KDL::Twist bounds = KDL::Twist::Zero());

private:
  KDL::ChainIkSolverVel_pinv vik_solver;
  KDL::ChainFkSolverPos_recursive fksolver;
};

3.1 执行逻辑

牛顿迭代初值seed赋值给q_init。以q_init为参数调用ChainIkSolverPos_TL::CartToJnt。“KDL：运动学求解器”中3公式已大致描述了逻辑。

q_init赋值给q_out。
fksolver.JntToCart(q_out, f)。用正向运动学方程算出此时末端关节位姿 ${fk_{1}}(q_1\cdots q_n)$ ，存储在f。
delta_twist = diffRelative(p_in, f)。算出此时位姿和期望位姿p_in间的误差delta_twist。注意，此时的delta_twist不是公式(3)中的 $E_{rr}$ ，而是一个可以和eps比较的Twist，详细见下面的“KDL::diffRelative”。
如果delta_twist小于误差阀值eps，认为求逆解成功，返回1。否则进入步骤5。
delta_twist = diff(f, p_in)。算出的delta_twist就是公式(3)中的 $E_{rr}$ 。
vik_solver.CartToJnt(q_out, delta_twist, delta_q)。求公式(3)中的状态增量 $J^{-1}\left[ Err \right]$ ，结果放在delta_q。
Add(q_out, delta_q, q_curr)。等价执行“q_curr = q_out + delta_q”。即q_curr存储着公式(3)的计算结果。
有一些判断逻辑，总的来说是把q_curr赋值给q_out。然后进入步骤2。

四、TRAC_IK::runNLOPT

NLopt是Nonlinear optimization的缩写，参考：NLopt--非线性优化--原理介绍及使用方法。

在runNLOPT，核心操作是调用NLOPT_IK::CartToJnt(...)。

<trac_ik>/nlopt_ik.hpp
------
enum OptType { Joint, DualQuat, SumSq, L2 };
class NLOPT_IK
{
public:
  int CartToJnt(const KDL::JntArray& q_init, const KDL::Frame& p_in, KDL::JntArray& q_out, const KDL::Twist bounds = KDL::Twist::Zero(), const KDL::JntArray& q_desired = KDL::JntArray());

private:
  OptType TYPE; // 固定使用NLOPT_IK::SumSq

  nlopt::opt opt; // 一个封装了nlopt功能的C++类
};

nlopt::opt是封装了nlopt功能的C++类，定义和实现都在nlopt.hpp。nlopt.hpp由nlopt-in.hpp自动生成。

4.1 执行逻辑

创建NLOPT_IK对象。期间会构造nlopt::opt对象opt，以下是opt构造函数中逻辑。

固定使用LD_SLSQP非线性优化算法。
opt.set_xtol_abs(tolerance[0])。设置优化结束条件，tolerance[0]值是boost::math::tools::epsilon<float>()。
TYPE值是SumSq。opt.set_min_objective(minfuncSumSquared, this)。

牛顿迭代初值seed赋值给q_init。以q_init为参数调用NLOPT_IK::CartToJnt。

opt.set_maxtime(maxtime)。
targetPose = p_in。p_in是client希望逆解的位姿。
opt.set_lower_bounds(artificial_lower_limits)。“artificial_lower_limits[i] = std::max(lb[i], best_x[i] - 2 * M_PI)”。artificial_lower_limits[i]存储着q[i]下限。lb[i]是urdf中设置是索引i关节角度下限，那best_x[i] - 2 * M_PI是啥概念？——可认为best_x就是q_init，从物理上说，下次最多转360度，所以下一次停在的角度不可能小于best_x[i] - 2 * M_PI。由于urdf一般会限制关节角度范围，导致不大可能360度都可用，std::max后的值时往往等于lb[i]。
opt.set_upper_bounds(artificial_upper_limits)。
opt.optimize(x, minf)。
如果步骤5逆解失败，时间也没溢出，那进入while循环，在每轮循环，随机生成一个q_in，记为变量x，调用opt.optimize(x, minf)执行nlopt优化。
能到这里，至少或时间溢出，或逆解成功。如果是逆解成功，best_x存储着求解出的q，把结果赋值给q_out，

在nlopt约束方面，有上、下边界约束，没有不等式、等式约束。

一次NLOPT_IK::CartToJnt执行至少一次nlopt优化。执行多次的条件是第一次没有求出逆解，时间上也没有超过溢出时间。执行后续优化时，除了初始参数x、溢出时间，其它参数和第一次一样。对初始参数x，来自一个随机生成的q_in。

4.2 minfuncSumSquared

目前trac_ik写死了TYPE=SumSq，对应使用的极小值函数是minfuncSumSquared。

double minfuncSumSquared(const std::vector<double>& x, std::vector<double>& grad, void* data)
{
  // Auxilory function to minimize (Sum of Squared joint angle error
  // from the requested configuration).  Because we wanted a Class
  // without static members, but NLOpt library does not support
  // passing methods of Classes, we use these auxilary functions.

  NLOPT_IK *c = (NLOPT_IK *) data;

  std::vector<double> vals(x);

  double jump = boost::math::tools::epsilon<float>();
  double result[1];
  c->cartSumSquaredError(vals, result);

输入参数x是此刻在用的关节状态。

jump趋于0，将作为 $\Delta x$ 。示例：1.1920928955078125e-07。

cartSumSquaredError算出位姿误差的级小值，具体数值是误差中6个分量的平方和。

  if (!grad.empty())
  {
    double v1[1];
    for (uint i = 0; i < x.size(); i++)
    {
      double original = vals[i];

      vals[i] = original + jump;
      c->cartSumSquaredError(vals, v1);

      vals[i] = original;
      grad[i] = (v1[0] - result[0]) / (2.0 * jump);

jump是 $\Delta x$ ，(v1[0] - result[0])是因为第i个关节值有了个 $\Delta x$ 微小变化后，对应误差发生的变化量 $\Delta f$ ，即第i个关节对误差的贡献率。grad[i]是导函数 $\Delta f / (2 * \Delta x)$ 的计算结果。此轮算出的grad将决定下一轮用的是什么q_in。

    }
  }

  return result[0];
}

void NLOPT_IK::cartSumSquaredError(const std::vector<double>& x, double error[])
{
  // Actual function to compute Euclidean distance error.  This uses
  // the KDL Forward Kinematics solver to compute the Cartesian pose
  // of the current joint configuration and compares that to the
  // desired Cartesian pose for the IK solve.

  if (aborted || progress != -3)
  {
    opt.force_stop();
    return;
  }



  KDL::JntArray q(x.size());

  for (uint i = 0; i < x.size(); i++)
    q(i) = x[i];

  int rc = fksolver.JntToCart(q, currentPose);

currentPose是关节状态是q时，末端关节的笛卡儿位姿。

  if (rc < 0)
    ROS_FATAL_STREAM("KDL FKSolver is failing: " << q.data);

  if (std::isnan(currentPose.p.x()))
  {
    ROS_ERROR("NaNs from NLOpt!!");
    error[0] = std::numeric_limits<float>::max();
    progress = -1;
    return;
  }

  KDL::Twist delta_twist = KDL::diffRelative(targetPose, currentPose);

targetPose是client希望到达的pose。while中每一次优化时，值不变。delta_twist用的类型是KDL::Twist，但语义不是速度，而是位姿变换量，也称位姿误差。位姿变化量有6个double分量，恰好Twist有6个double字段，于是就把xyz放在Twist.vel，“rpy”在Twist.rot，应该不是欧拉角rpy，但应该是和旋转有关的3个分量，暂用加引号的“rpy”表示。delta_twist表示targetPose和currentPose之间的变换量，方向是从currentPose到targetPose，还是反过来，不能确定。具体到6个分量，假设以“e_”为前辍的，是类型由KDL::Frame变化到Eigen::Isometry3d、值不变的变量，那xyz值相当于取“e_targetPose.inverse() * e_currentPose”的平移部分。至于怎么算“rpy”，没有理解。

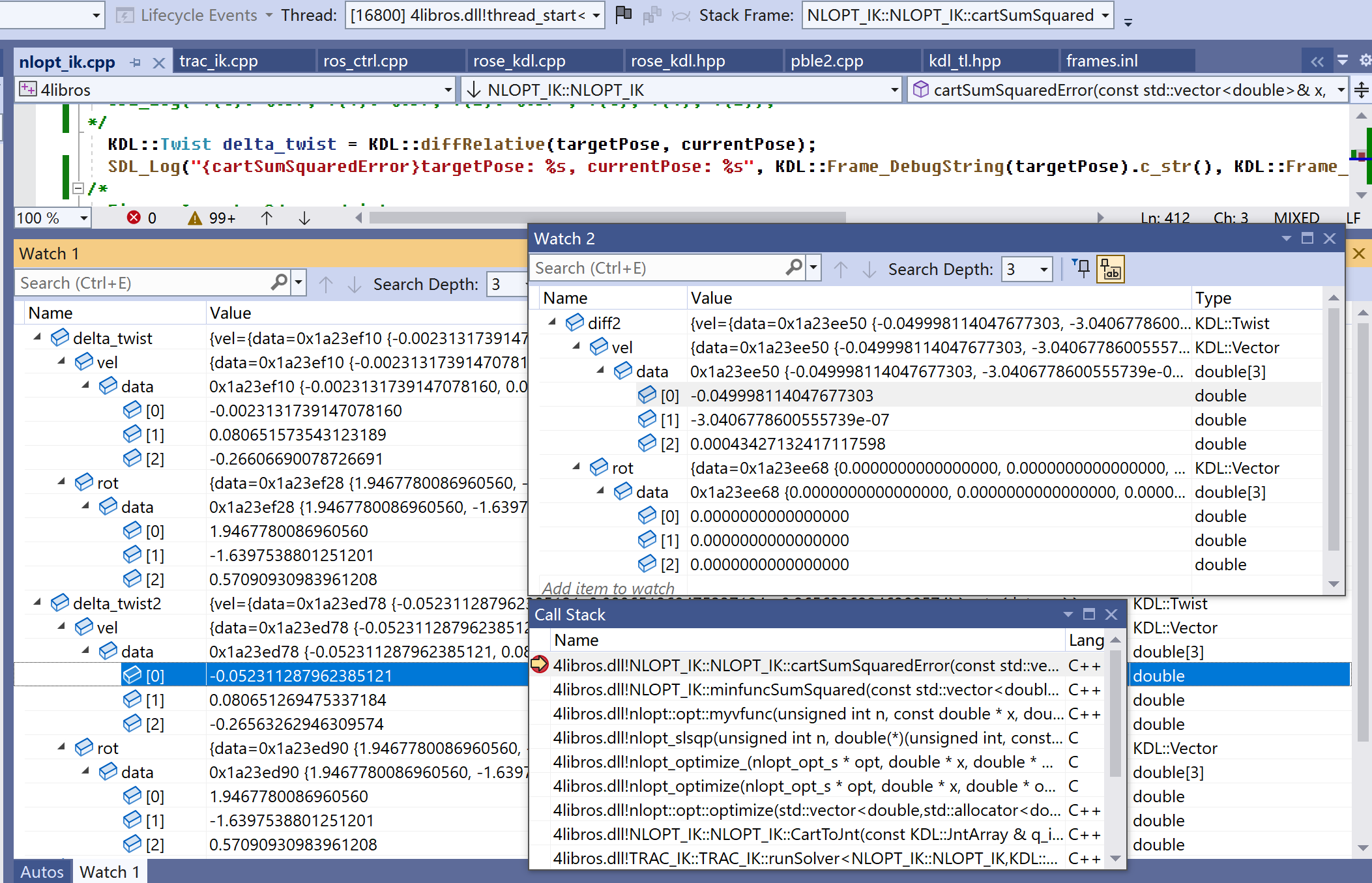
当两个输入位姿存在不同旋转时，diffRelative计算出的平移差不是两个输入位姿的平移对应分量的差值，会有一个微小变动。举个例子，以x、y、z对应三分量相减的平移差是[0.003370, 0.002000, 0.000119]，diffRelative算出的平移差会是[0.002651, 0.002000, 0.002084]。

diffRelative算出的delta_twist中，可认为targetPose中的x分量只影响对应的delta_twist.vel(0)，即使对其它分量有影响，影响值也在0.0005以内。让看个示例。

currentPose: {p:(-0.00028, 0.04860, 0.01189), M:(2.15437, -1.36582, 2.55894)}
targetPose: {p:(-0.00029, -0.07871, 0.25905), M:(-0.77001, -0.00623, -3.13555)}

给targetPose的x增加“-0.05”，其它不变，记为targetPose2。

targetPose2: {p:(-0.05028, -0.07871, 0.25905), M:(-0.77001, -0.00623, -3.13555)}

然后分别计算它们和同一个currentPose的diffRelavite。

delta_twist = KDL::diffRelative(targetPose, currentPose);
delta_twist2 = KDL::diffRelative(targetPose2, currentPose);

图1的Watch1显示了delta_twist和delta_twist2，Watch2中diff2则来自“delta_twist2 - delta_twist”，即显示了这两个Twist差值。由diff2可看到，两次diffRelative，rot部分没变化，vel.x保持“原x差值”-0.05，vel.y差值可认为0，vel.z差值在0.0005以内。

  for (int i = 0; i < 6; i++)
  {
    if (std::abs(delta_twist[i]) <= std::abs(bounds[i]))
      delta_twist[i] = 0.0;
  }

  error[0] = KDL::dot(delta_twist.vel, delta_twist.vel) + KDL::dot(delta_twist.rot, delta_twist.rot);

误差中6个分量的平方和做为目标函数的值，即 $\sum_{n=1}^{3}{delta\_twist.vel(n)^{2}} + \sum_{n=1}^{3}{delta\_twist.rot(n)^{2}}$ 。也就是说，优化是要算出位姿误差的极小值，具体数值是误差中各分量的平方和。

变量bounds称为改0阈值，作用见下文的“只要满足平移(position_ik_=true)”。它是caller调用TRAC_IK::CartToJnt(...)这个api时传下的参数，用于判断出该分量上的误差<=它时，强行改为0。换句话说，让caller不改eps前提下，有机会可以加大某些分量的允许误差。有了bounds[0]可自设定x归0误差，加上上面“targetPose.x只影响delta_twist.x”这个结论，有人会想到这么一种可能：caller在设置要逆解的位姿时，任意指定一个x，其它yzrpy则是正确的，然后再把这里bounds[0]设为足够大，即不管diffRelative算出的delta_twist[0]是何值，到这里delta_twist[0]都归到0，是不是就能做到不用设对x就可算出逆解？——不行。由delta_twist算出的error[0]将用于计算后面导函数误差 $\Delta f$ ，它应该正确、灵敏反应出不同 $q$ 值时的变化。一旦不正确或不灵敏，会影响nlopt的收敛速度，结果造成时间溢出，逆解失败。举个例子，第i次迭代的关节状态是 $q_{i}$ ，算出的error[0]是 $error_{i}$ ，下一次 $q_{i+1}$ 时算出的误差是 $error_{i+1}$ ，值上 $error_{i+1}$ 小于 $error_{i}$ ，即误差变小了，但如果加上各自的delta_twist[0]， $error_{i+1}$ 其实大于 $error_{i}$ ！一旦出现这情况，基本可认定此次不可能求出逆解。

  if (KDL::Equal(delta_twist, KDL::Twist::Zero(), eps))
  {
    progress = 1;
    best_x = x;
逆解成功。preogress置为1，best_x存储着逆解出的关节状态。
    return;
  }
}

五、只要满足平移(position_ik_=true)

位姿有6个变量，3个平移和3个旋转，求逆解时，需要同时满足这6个变量。在一些场合，只须要满足平移，可忽略旋转。track_ik考虑到这种需求，用了一个叫position_ik_变量，是true时，表示此次求逆解只须满足平移。

5.1 误差改0阈值：KDL::Twist bounds

一旦只要满足平移时，调用者会把bounds的旋转部分阈值置为最大数值。

bool TRAC_IKKinematicsPlugin::searchPositionIK(const geometry_msgs::Pose &ik_pose, ...)
{
  ...
  KDL::Twist bounds = KDL::Twist::Zero();
  if (position_ik_)
  {
    bounds.rot.x(std::numeric_limits<float>::max());
    bounds.rot.y(std::numeric_limits<float>::max());
    bounds.rot.z(std::numeric_limits<float>::max());
  }
  ...
}

bounds不是各变量的容许误差。它的作用是，当变量的误差小于它时，就改为0。置0，是希望达到这么个目标，让导数变成0，相当于发生在该变量上的 $\Delta x$ 对 $\Delta f$ 没有贡献。上面把bounds的旋转部分阈值设置为最大数值，意味着不论roll、pitch、yaw误差是多少，误差都要改为是0

5.2 只需要满足平移时的ChainIkSolverPos_TL

trac_ik会同时运行ChainIkSolverPos_TL和NLOPT_IK这两个ik，测试下来，只需要满足平移时，NLOPT_IK能正常工作，也就是说，能正确找到个只须满足平移的逆解，但ChainIkSolverPos_TL不行。深入代码，对如何使用bounds，ChainIkSolverPos_TL只是做了个判断，当该分量上比较下来的误差小于bounds，就改为0。这个改为0后，只是用在最后和容许误差比较时，并没有体现在导数上，即雅可比矩阵。

在NLOPT_IK，bounds发生作用是在cartSumSquaredError，当该分量上比较下来的误差小于bounds，对应的delta_twist[i]就改为0。这6个分量delta_twist[i]平方和可认为是 $\Delta f$ 。置0操作，相当于该分量上的 $\Delta x$ 对 $\Delta f$ 没贡献，即导数是0。

导数是放在雅可比矩阵，于是想到一种方法，在计算雅可比矩阵时，让和旋转三变量相关的总是0。

<orocos_kdl>/src/chainjnttojacsolver.cpp
------
int ChainJntToJacSolver::JntToJac(const JntArray& q_in, Jacobian& jac, int seg_nr)
{
  .....
  if (position_ik_) {

算出雅可比矩阵(jac)后，如果只需满足平移，调用ZeroOrientation()，把旋转相关的3行置0。

    jac.ZeroOrientation();
  }
  return (error = E_NOERROR);
}

<orocos_kdl>/src/jacobian.cpp
------
void Jacobian::ZeroOrientation()
{
    // set line[3..5] to zero
    int cols = data.cols();
    for (int row = 3; row < 6; row ++) {
        for (int col = 0; col < cols; col ++) {
            data(row, col) = 0;

变量data的类型Eigen::Matrix<double,6,Eigen::Dynamic>，是个6行矩阵。从上到下，依次是平移x、y、z，旋转roll、pitch、yaw。

        }
    }
}

Jacobian::ZeroOrientation是个新增函数。

全部评论: 0 条