makePlan使用的是静态地图+实时障碍层,这个静态地图会和此时地图有所不同,像同一坐标值出现偏差。换句话说,makePlan中的LETHAL_OBSTACLE栅格,在此时地图可能变成INSCRIBED_INFLATED_OBSTACLE。
在ros官方设计中,makePlan是通过膨胀层(内切圆半径,图1青色格子),使得得到的路径考虑了机器人足迹。但我把青色格子语义变成了相邻障碍的危险栅格,使得makePlan得到的是没考虑机器人足迹的路径。这里需得到一条考虑了足迹的local_path。

二、a_star_search
a_star_search用于搜出一条从src到origin_dst的最佳路径。针对图2示例,源栅格src是(28, 28),目标栅格dst是(39, 10),要通过A*算法搜出一条从(28, 28)到(39, 39)的最“佳”路径。
- 将起始结点src放入OPEN表pq。
- 如果pq表不为空,从表头取一个结点n,如果为空算法失败
- n是目标解吗?1)不是,进入步骤4。2)是,成功找到一个解。算法结束。
- 展开和n相邻的8个结点。对每个衍生结点next,坐标记为i_loc,挨个进行下面操作。
4.1. 用代价函数算出i_loc上代价,记为cost。
4.2. cost加上n.g得到next.g,如果这个next.g比“上次”更好,就将它们放入pq,并把pq按代价排序,最小的放在表头,这个最“佳”节点将作为下一次判断的当前结点。 - 处理完8个next后,转去步骤2。
算法只使用OPEN表,没有CLOSE表。变量pq表示OPEN表,它是个有序表,每个单元表示一个结点n,按着n.t进行排序,表示起始结点若经过它,到达dst需要的代价t(n)。
如果orign_dst就是障碍物栅格(LETHAL_OBSTACLE),那a_star_search就不可能找到src到origin_dst路径。考虑到足迹要占用数个栅格,这时orign_dst在内切圆半径的那些栅格也不可能是dst。加上adjust_global_plan使用a_star_search只是要找到一条更优路径,不要求一定那到达原local_path的目标点。变量sq_max_stop_dist表示这个dst到origin_dst的容许距离,为减少开根号次数,前缀“sq_”表示这个平方值。
2.1 a_star_search源码
- src。起始结点。
- origin_dst。目标结点。变量名没用dst,是因为最终得到的路径结点可能不是origin_dst。在函数中,真正的目标结点才记为dst。
- stop_at。失败阈值。不断搜索,最优结点n.g也已超过这值了,认为此次搜索失败。
- calc。代价函数。既不是g(n),也不是h(n),是计算机器人在栅格n上的代价。对栅格n上代价,会立刻联想到可直接得到某个栅格代价的costmap。可机器人面积往往大于resolution*resolution,那它在该栅格上代价就是以n作为机器人中心点、包括其它涉及到栅格的某种代价“和”。至于怎么得到“涉及到栅格”,可借助机器人的内切圆半径。目前代价函数:以n为中心,涉及到的((cell_inscribed_radius - 1) * 2 + 1) * ((cell_inscribed_radius - 1) * 2 + 1)个栅格的平均代价,即这些栅格的代价和除以个数。
- costmap。局部代价地图。
- cell_inscribed_radius。以栅格数表示的内切圆半径。示例:3。
- exclusion_rect。一个矩形形状的禁止区域。旧路径已有一定形状,新路径只可能沿着它进行优化。对图1,机器人坐标系下,路径应该基本在第4象限,或可能进第1象限。这时可以把位在第2象限的{0, 40, 20, 20}设为禁止区域。这一来避免让机器人在进这区域进行寻路,二来可以减少点计算量。
plain_route a_star_search(const SDL_Point& src, const SDL_Point& origin_dst, double stop_at,
const cost_calculator& calc, const costmap_2d::Costmap2D& costmap,
int cell_inscribed_radius, const SDL_Rect& exclusion_rect)
{
const int width = costmap.getSizeInCellsX();
const int height = costmap.getSizeInCellsY();
//----------------- PRE_CONDITIONS ------------------
VALIDATE(width > 0, null_str);
VALIDATE(width == height, null_str);
VALIDATE(cell_inscribed_radius > 0, null_str);
//---------------------------------------------------
if (stop_at == 0) {
stop_at = calc.default_stop_at(width);
}
// A* search: $src -> $dst
SDL_Point dst = origin_dst; // dst maybe change
int inscribeds;
double sq_max_stop_dist = -1; // -1
double dst_cost = calc.cost(dst, inscribeds);
// calculate dst's cost, must use block.
if (dst_cost == calc.NoPathValue || dst_cost == calc.NoInformation) {
sq_max_stop_dist = (cell_inscribed_radius + 1) * (cell_inscribed_radius + 1);
} else if (dst_cost == calc.InscribedInflatedObstacle) {
sq_max_stop_dist = (cell_inscribed_radius - 1) * (cell_inscribed_radius - 1);
}根据目标结点origin_dst不同情况,算出不一样的容许距离sq_max_stop_dist。
costmap_2d::MapLocation locs[8];
// increment search_counter but skip the range equivalent to uninitialized
search_counter += 2;
if (search_counter - bad_search_counter <= 1u) {
search_counter += 2;
}
全局变量search_counter加2。而且要避免出现0(bad_search_counter)或1。后文“search_counter和in字段”有解释search_counter。
reallocate_pq(width, height); static std::vector nodes; nodes.resize(width * height); // this create uninitalized nodes indexer index(width, height); comp node_comp(nodes); nodes[index(dst)].g = stop_at + 1;
1/3[dst.g]:设置[dst.g]的初值为stop_at + 1。
nodes[index(src)] = node(0, src, SDL_Point{nposm, nposm}, dst, costmap);
// rember destination cost.
// is destination is all, don't remember! make below code find out right path.
// [see remark#40]
hash[index(dst)].in = search_counter;
hash[index(dst)].cost = dst_cost;
std::vector<int> pq;
pq.push_back(index(src));
const int costmap_cells = width * height;
while (!pq.empty()) {
node& n = nodes[pq.front()];
n.in = search_counter;
std::pop_heap(pq.begin(), pq.end(), node_comp);
pq.pop_back();
if (n.t >= nodes[index(dst)].g) {
break;除pq.empty()外,只有这里能跳出while,进入这里有多种情况。
- 寻路成功。3/3[dst.g]:经过“2/3[dst.g]”,dst.g已由初值“stop_at + 1”改为next那时算出的“cost”,n正好是那时的next,这个等式自然成立。
- 寻路失败。dst.g保持着初值stop_at + 1,但最佳节点n.t就已经超过它了。最佳都这样,那不必再找了。
为什么用n.t,而不是n.g?第一种情况寻路成功时,之前已经过“2/3[dst.g]”,用n.t还是n.g没区别。若是第二种情况寻路失败,用n.t有助于更快中止寻路。“快”是什么速度取决于n.h,即heuristic(...)算出的代价。
}
// last_location = n.curr;
const int count = costmap.getMax8Cells(n.curr.x, n.curr.y, locs);
for (int i = 0; i < count; i++) {
const int i_index = index(locs[i].x, locs[i].y);
VALIDATE(i_index >= 0 && i_index < costmap_cells, null_str);
const SDL_Point i_loc{(int)locs[i].x, (int)locs[i].y};
if (SDL_PointInRect(&i_loc, &exclusion_rect)) {
continue;
}
node& next = nodes[i_index];
double threshold = (next.in - search_counter <= 1u) ? next.g : stop_at + 1;
// cost() is always >= 1 (assumed and needed by the heuristic)
if (n.g + 1 >= threshold) {
continue;进入这里分两种情况。
- next已经被某个n衍生到过,next.g是那次算出的g。这里要注意一个规则,对一个节点next,最多可能从8个方向衍生到它。当被衍生到一次后,可能还有第二次、第三次。程序会保证每个栅格上代价至少是1。进入这里意味着此次衍生肯定不会比上次更好了,没必要再考虑next。
- next没被衍生到过,但n.g已经是stop_at,到它就超过失败阈值,没必要再考虑next。
由于stop_at往往设的是一个较大值,能进入这里往往的是第一种情况。
}
double cost;
if (hash[i_index].in == search_counter) {
cost = hash[i_index].cost;之前已算过next在自个坐标上cost,从hash查找表拿就行。
} else {
cost = calc.cost(i_loc, inscribeds);
{
hash[i_index].in = search_counter;
hash[i_index].cost = cost;
}之前没算过next在自个坐标上cost,用代价函数进行计算,并把结果存入hash查找表。
}
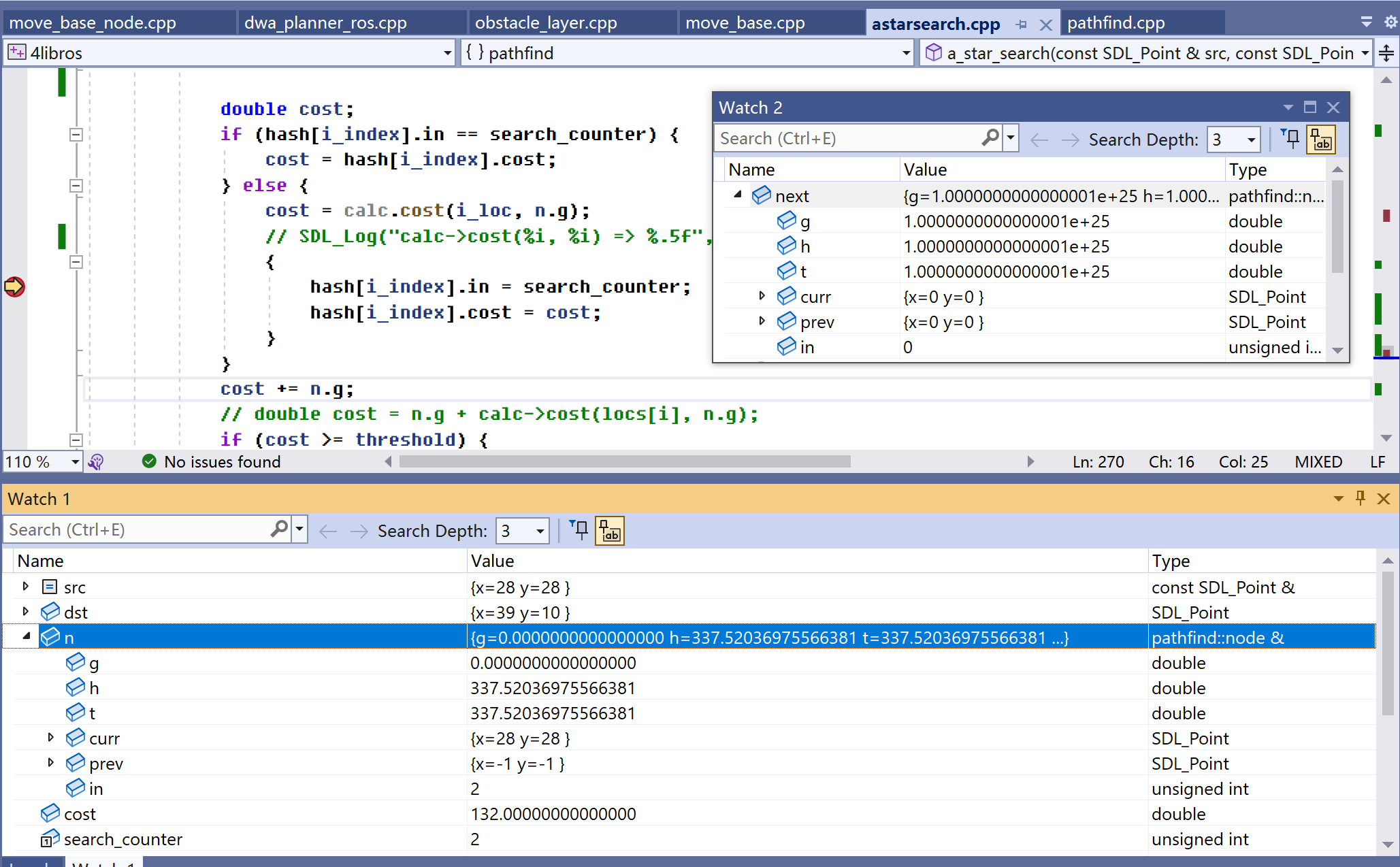
变量n、next表示节点,它们类型是node、其中的t、g、h分别表示f(n)=g(n)+h(n)中的f、g、h计算出的double值。注:t、g、h默认值是1e25,即10的25次方,见Watch2中保留着初始值的next。
n是当前正在处理的节点,它总是此刻认为能找到目标解的最佳节点。当然,此刻它已离开pq。
next是由n衍生出的节点,即n相邻8个节点中的一个。接下就会把它的t、g、h赋值,并放入pq
cost += n.g;
// double cost = n.g + calc->cost(locs[i], n.g);
if (cost >= threshold) {
continue;
}
// may change dst?
int x_diff = locs[i].x - origin_dst.x;
int y_diff = locs[i].y - origin_dst.y;
const int sq_dist = x_diff * x_diff + y_diff * y_diff;
if (sq_dist <= sq_max_stop_dist) {
dst.x = locs[i].x;
dst.y = locs[i].y;
// why -0.1? --make late sq_dist not enter here.
sq_max_stop_dist = sq_dist - 0.1;
}
bool in_list = next.in == search_counter + 1;
next = node(cost, i_loc, n.curr, dst, costmap);2/3[dst.g]:如果next恰好是dst,那会修改dst.g,值变成这里算出的cost。
if (in_list) {
std::push_heap(pq.begin(), std::find(pq.begin(), pq.end(), i_index) + 1, node_comp);
} else {
pq.push_back(i_index);
std::push_heap(pq.begin(), pq.end(), node_comp);
}
}
}
plain_route route;
if (nodes[index(dst)].g <= stop_at) {
route.move_cost = static_cast<int>(nodes[index(dst)].g);
for (node curr = nodes[index(dst)]; curr.prev.x != nposm; curr = nodes[index(curr.prev)]) {
route.steps.push_back(curr.curr);
}
route.steps.push_back(src);
std::reverse(route.steps.begin(), route.steps.end());
} else {
// aborted a* search
route.move_cost = static_cast<int>(calc.NoPathValue);
}
release_pq();
return route;
}
2.2 push_heap、pop_heap
使用push_heap、pop_heap,目的是确保pq这个数组是个有序open表。pq这个数组的单元值是int,表示结点索引,越往后,其对应结点的t(g+h)越大。
push_heap
用于将堆底单元加入已排序堆结构中。
因为make_heap只能建堆,如果当前堆数据发生改变,就需要使用push_heap重回大堆/小堆。值得注意:first 到 last-1 之间的元素必须满足堆结构。它仅仅是将last之前元素插入堆中。意思就是,如果一次性插入多个元素,它只会把最后一个元素(堆底)加入堆结构中。
其参数与make_heap相同,不再赘述。
pop_heap
pop_heap(_RAIter,_RAIter) 默认为大顶堆。该函数作用是“删除”堆顶元素。为什么加引号——因为就像堆排序那样,所谓删除只是将堆顶元素移至堆底。
pop_heap(_RAIter,_RAIter,_Compare) _Compare有两种参数,一种是greater(小顶堆),一种是less(大顶堆)
比如pop_heap(nums.begin(), nums.end(),greater<int>()),它会将堆顶元素(即为数组第一个位置)和数组最后一个位置对调,然后你可以调用数组pop_back,删除这个元素
注意,pop_heap中的_Compare和make_heap中的_Compare参数必须是一致的,不然会失败
2.3 hash表
为什么要用hash?——计算i_loc上的cost较花时间。而在此次寻路过程中,这个cost是不会变的。那把i_index->cost做成一个查找表,这个查找表就是hash。一旦i_index已算出过cost,通过hash,下次以i_index为key就可搜到cost。
2.3 search_counter和in字段
search_counter是个全局变量,有着以下特点。
- 类型是uint32_t。
- 只会是偶数,但不会是0。
- 每次进入a_star_search时,会加2。之后在a_star_search期间,值就不会变了。所以虽然初值是0,但在a_start_search看来,可认为初值是2。
- 不断执行a_star_search,每次就会加2,迟早会到达uint32_t最大值,然后回转,这时会跳过0,进入2。
存在两种in字段:nodes[i_index].in和hash[i_index].in,类型和search_count一样,都是uint32_t。
nodes[i_index].in
nodes类型是std::vector<node>,为提高效率,把它作为全局变量。以下是一次a_star_search过程中,in和search_counter关系。
- 第一次进入a_star_search时in会置为0。之后就是上次a_star_search之后是什么值,此次就是什么值。
- 访问过、并放入pq表的结点会被置为in=search_counter+1。这里访问指的是src和衍生。
- 该结点移出pq表、要用于分析了,会被置为in=search_counter。
in变量用于判断某一栅格在此次a_star_search时是否已被访问过,判断代码是“(in - search_counter <= 1u)”,返回true意味着已访问过,否则没有。此次a_star_search没被访问过时,in值是不确定的,这个式子中in可能比search_counter小,但因为是无符号数减法,判断还是返回false,结论是没访问过。举个例子,in是11,search_counter是12,相减后的值4294967295(0xffffffff),不满足“<=1u”。
要满足“(in - search_counter <= 1u)”,意味着in必须大于等于search_counter,大于时差值只能是1。上面已说过,这两种情况都表示该栅格已访问过,区别在于,1时该结点没在pq表,0则正在pq表。
对in变量,要标志node是否访问过,用个bool变量不是更简单,干吗要in又要search_counter,这不是增加复杂度吗?——这么做原因是nodes是个静态变量,nodes中的元素数是地图格子数,用in、search_counter是为省去第“二”次及以后的初始化nodes时间。因为不初始化nodes,第N+1次a_star_search用的是第N次操作后形成的nodes,N+1次的in值自然也要基于N次in值,而那个in值将“小于”此次search_couter。
和in状态相关的另一个可能疑问,函数每次搜索前会调用nodes.resize,nodes.resize会不会把所有in复位为0?——不会。以下是resize的函数实现。
void resize(size_type new_size) { resize(new_size, T()); }
void resize(size_type new_size, const T& x)
{
if (new_size < size()) {
erase(begin() + new_size, end()); // erase区间范围以外的数据,确保区间以外的数据无效
} else {
insert(end(), new_size - size(), x); // 填补区间范围内空缺的数据,确保区间内的数据有效
}
}hash[i_index].in
- 初始时全是search_counter - 2。reallocate_hash(...)负责初始化这些值。
- 该栅格计算过代价,被赋值上值后,变成search_counter。
- 不会出现search_counter+1。用“hash[i_index].in == search_counter”来判断此次是否被赋过值。
现在hash其实可认为就是函数内变量。要表示hash[i_index]是否计算过代价,用个bool变量就行了。用in、search_counter,是在想将来或许会把hash作为全局变量吧。