一、find_routes概述
find_routes根据单位所在格子和可用移动力计算出单位的可到达位置。
当在游戏中单击鼠标左键选中一个单位,这时地图上显示该单位可到达位置。find_routes就用于计算这些个位置。下图就是鼠标单击(33,12)处时显示的可到达位置,总计有35个(不包括(32,11)和(32,12)这两个站了敌方单位的格子)。
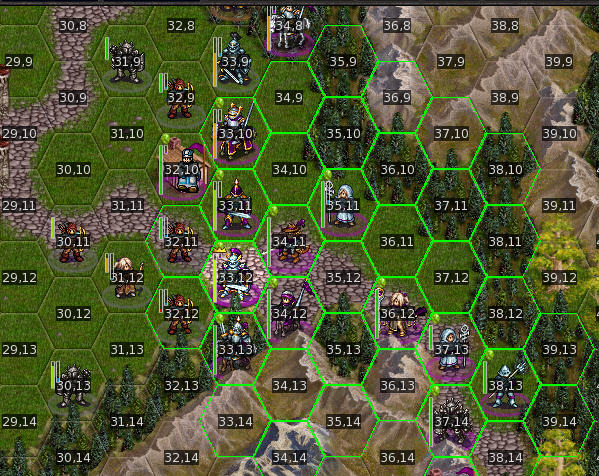
find_routes计算这些个位置时采用A*搜索算法。既然使用了A*算法则需要明确几个问题:
满足什么样条件的结点才能放入OPEN:如果A点是第一次遇到,只要该点不站敌方单位或有移动力移到该点则可放入;如果A点是已经访问过,则此次展开要能比过去更“优”才能放入。
估值函数:到达A点剩余移动力比到达B点剩余移动力多,则认为到达A点价值更高。
已经展开但没有访问的结点集的变量表示:pq
已访问的结点集:这个没有确切定义,nodes很大部分完成这个功能。
以上图为例叙述搜索过程。
第一次
初始状态:
OPEN: (33,12)
CLOSE:
正访问结点:(33,12)
进入启发式搜索。具体来说就是判断欲访问结点(33,12)周围六个节点能不能展开,及形成该节点状态。
(32,11):站着个敌方单位,不能展开。(图中也变成可移动框,那是接下的show_attack_options加入的)
(32,12):站着个敌方单位,不能展开。
(33,13):能展开,但由于处在(32,12)的ZOC内,剩余移动力0。该点状态:{C(33,13), P(33,12), 0}。
(34,12):能展开。该点状态:{C(34,12), P(33,12), 6}。
(34,11):能展开。该点状态:{C(34,11), P(33,12), 6}。
(33,11):能展开。该点状态:{C(33,11), P(33,12), 6}。
OPEN: (33,13), (34,12), (34,11), (33,11)
对OPEN中结点进行排序,剩余移动力最大的排在前面。
结末状态:
(34,12), (34,11), (33,11), (33,13)
CLOSE: (33,12)
第二次
正访问结点:(34,12)
进入启发式搜索。
(33,12):不能展开。该结点已访问过,而且已访问过的剩余移动力7比到(34,12)都大。
(33,13):不能展开。该结点已访问过,且此次并不比已存在“优”。
(34,13):能展开。该点状态:{C(34,13), P(34,12), 3}。(移动山地花费3点移动力)
(35,13):能展开。该点状态:{C(35,13), P(34,12), 4}。
(35,12):能展开。该点状态:{C(35,12), P(34,12), 5}。
(34,11):不能展开。该结点已访问过,且此次并不比已存在“优”。
结末状态:(OPEN已被排序)
OPEN: (34,11), (33,11), (35,12), (35,13), (34,13), (33,11)
CLOSE:
第三次
第N次也是前面一样流程,在此次详述下for中的四个if判断。
正访问结点:(34,11),它展开出的第一个结点:(33,11),(33,11)已经被访问过。
第一个if:(next_visited && !(n < next)),起点到(34,11)不优于起点到(33,11)。如果到(34,11)要花费移动力不会比到(33,11)少,那可以肯定没必要再寻(34,11)到(33,11)这条路了。
第二个if:(t.movement_left < move_cost || t.turns_left < 0)。t是(33,12)-->(34,11)剩余移动力(注:没到(33,11)),(33,12)单位在(34,11)时已没再有移动力到达(33,11),那么这条路径自然不能成立。
第三个if:(next_visited && !(t < next)):t是(33,12)-->(34,11)-->(33,11),起始经过这条路径到达(33,11)不优于已存的起点到(33,11),那这条路径也不必找了。
第四个if:(next_visited && !(t < next))。这个第三个if是一样判断,但到这时t经过了单位考虑,一旦t位在敌方zoc内,t的剩余移动力归零。以上正是这种情况,(31,11)站着个敌方单位,所以(34,11)到(33,11)后,移动力就归零。——由于个if,!(t < netx)成立,continue。===》在node处依旧保存着curr=(33,11),prev=(33,12), left_movement=0。
二、find_routes FAQ
node中in字段
说到in字段则必须说search_counter变量。search_counter是一个全局变量,但在一次find_routes过程中它的值保持不变。search_counter最小值是2(不可能是0和1)。
in变量用于判断某一格子在此次find_routes时是否已被访问过。此次find_routes没被访问过时,值是不确定的,但满足:1)是偶数;2)(in - search_counter <= 1u)成立,这个式子中in可能比search_counter小,但因为是无符号数,<还是成立。
对in变量,要标志node是否访问过,用个bool变量不是更简单,干吗要in又要search_counter,这不是增加复杂度吗?——这么做原因是nodes是个静态变量(node中的元素数是地图格子数,初始化须要点时间)。第N+1次用的是第N次操作结果,N+1次的in值自然也要基于N次in值。
要用bool变量标识的话,逃不掉各个node中开辟个状态变量方法,这个变量在搜索前全部置为false,访问过后置为true。用了以上in+serach_counter方法后,省略了这个全置false过程。
和in状态相关的另一个可能疑问,函数每次搜索前会调用nodes.resize,nodes.resize会不会把所有in复位为0?
——不会。以下是resize的函数实现:
void resize(size_type new_size) { resize(new_size, T()); }
void resize(size_type new_size, const T& x)
{
if (new_size < size()) {
erase(begin() + new_size, end()); // erase区间范围以外的数据,确保区间以外的数据无效
} else {
insert(end(), new_size - size(), x); // 填补区间范围内空缺的数据,确保区间内的数据有效
}
}
三、find_routes函数
@map:全局唯一的gamemap;
@uinits:全局唯一的unit_map;
@u:要从它开始计算可到达位置的单位;
@loc:一个坐标值,要以它为起点开始计算可到达位置;
@move_left:单位的剩余移动力。对于未移动过单位,它的值就是unit.total_movement;
@[color=Red]destinations[/color][OUT]:存储计算出可到达位置。destinations值上可认为是step数组,struct step定义:{(map_location) prev, (map_location) curr, (int) move_left};
@force_ignore_zoc:是否强制不考虑zoc。ignore_units=true时,该值忽略;
@allow_teleport:是否要使用传送。拥有传送技能单位该值一般置true,否则false;
@viewing_team:本阵营可看见的其它阵营(包括自己),它经常等于teams;
@additional_turns:附加回合数。1:显示两回内数径,2:显示三回内路径;
@see_all:默认置false;
@ignore_units:是否忽略单位,默认false;
格子一旦被访问过,它的in值被置为search_counter + 1。
经过find_routes后形成的destinations内容
1、自已所在格子。即loc,也会在destinations中,但它的step.prev是个未定义值;
2、友方阵营单位所在格子。
3、单位有传输技能时,即allow_teleport,***
4、敌方阵营单位所在格子不在destinations中,(ignore_units=false)。上面包括两个敌方单位格子,那个后面的show_attack_options(u)添加的。
5、排序。以[X][Y]次序,x、y都0逐增。
static void find_routes(const gamemap& map, const unit_map& units,
const unit& u, const map_location& loc,
int move_left, pathfind::paths::dest_vect &destinations,
std::vector<team> const &teams,
bool force_ignore_zocs, bool allow_teleport, int turns_left,
const team &viewing_team,
bool see_all, bool ignore_units)
{
const team& current_team = teams[u.side() - 1];
std::set<map_location> teleports;
if (allow_teleport) {
teleports = pathfind::get_teleport_locations(u, units, viewing_team, see_all, ignore_units);
}
const int total_movement = u.total_movement();
// prepare self-city grid condition
// 得到属于“本城格子”判断条件
void* expediting_city_cookie = NULL;
if (units.expediting()) {
expediting_city_cookie = units.expediting_city_node();
} else if (units.city_from_loc(loc)) {
expediting_city_cookie = units.get_cookie(loc);
}
std::vector<map_location> locs(6 + teleports.size());
std::copy(teleports.begin(), teleports.end(), locs.begin() + 6);
search_counter += 2;
if (search_counter == 0) search_counter = 2;
static std::vector<node> nodes;
nodes.resize(map.w() * map.h());
indexer index(map.w(), map.h());
comp node_comp(nodes);
int xmin = loc.x, xmax = loc.x, ymin = loc.y, ymax = loc.y, nb_dest = 1;
nodes[index(loc)] = node(move_left, turns_left, map_location::null_location, loc);
std::vector<int> pq;
// 调用程序可能把move_left=0传下来,像出征,这时不要让出征到“本城格子”。为不显示“本城格子”是可出征地,办法就是让move_left=0时不执行接下的while循环体
if (move_left || turns_left) {
pq.push_back(index(loc));
}
while (!pq.empty()) {
node& n = nodes[pq.front()];
std::pop_heap(pq.begin(), pq.end(), node_comp);
pq.pop_back();
n.in = search_counter;
get_adjacent_tiles(n.curr, &locs[0]);
for (int i = teleports.count(n.curr) ? locs.size() : 6; i-- > 0; ) {
if (!locs[i].valid(map.w(), map.h())) continue;
node& next = nodes[index(locs[i])];
bool next_visited = next.in - search_counter <= 1u;
// Classic Dijkstra allow to skip chosen nodes (with next.in==search_counter)
// But the cost function and hex grid allow to also skip visited nodes:
// if next was visited, then we already have a path 'src-..-n2-next'
// - n2 was chosen before n, meaning that it is nearer to src.
// - the cost of 'n-next' can't be smaller than 'n2-next' because
// cost is independent of direction and we don't have more MP at n
// (important because more MP may allow to avoid waiting next turn)
// Thus, 'src-..-n-next' can't be shorter.
if (next_visited) continue;
int move_cost;
if (expediting_city_cookie && units.get_cookie(locs[i]) == expediting_city_cookie) {
// locs[i]是“本城格子”,消耗移动力0
move_cost = 0;
} else {
move_cost = u.movement_cost(map[locs[i]]);
}
node t = node(n.movement_left, n.turns_left, n.curr, locs[i]);
if (t.movement_left < move_cost) {
t.movement_left = total_movement;
t.turns_left--;
}
// 前半部分作用:有些单位的total_movement可能就小于在该地形上的需要移动力,即使加了一回合还是不够
if (t.movement_left < move_cost || t.turns_left < 0) continue;
t.movement_left -= move_cost;
if (!ignore_units) {
const unit *v =
get_visible_unit(units, locs[i], viewing_team, see_all);
if (v && current_team.is_enemy(v->side())) {
// 正欲展开格子上站着个敌方单位,该格子不进入OPEN
continue;
}
// move cost in any terrain cannot be zero. it is zero indicate loc is self-city grid.
if (move_cost && !force_ignore_zocs && t.movement_left > 0
&& pathfind::enemy_zoc(units, teams, locs[i], viewing_team, u.side(), see_all)
&& !u.get_ability_bool("skirmisher", locs[i])) {
// 正欲展开格子在一个敌方单位的ZOC内,一旦移动到该格子剩余移动力置0。
t.movement_left = 0;
}
}
// 确定要展开一个新的格子后,看是否要扩大容纳可到达位置的“矩形”
++nb_dest;
int x = locs[i].x;
if (x < xmin) xmin = x;
if (xmax < x) xmax = x;
int y = locs[i].y;
if (y < ymin) ymin = y;
if (ymax < y) ymax = y;
bool in_list = next.in == search_counter + 1;
t.in = search_counter + 1;
next = t;
// if already in the priority queue then we just update it, else push it.
if (in_list) { // never happen see next_visited above
std::push_heap(pq.begin(), std::find(pq.begin(), pq.end(), index(locs[i])) + 1, node_comp);
} else {
pq.push_back(index(locs[i]));
std::push_heap(pq.begin(), pq.end(), node_comp);
}
}
}
// Build the routes for every map_location that we reached.
// The ordering must be compatible with map_location::operator<.
// 根据容纳可到达位置的“矩形”,以X第一次排序Y第二次排序顺序从nodes生成destinations
destinations.reserve(nb_dest);
for (int x = xmin; x <= xmax; ++x) {
for (int y = ymin; y <= ymax; ++y)
{
const node &n = nodes[index(map_location(x, y))];
if (n.in - search_counter > 1u) continue;
pathfind::paths::step s =
{ n.curr, n.prev, n.movement_left + n.turns_left * total_movement };
destinations.push_back(s);
}
}
}
四、a_star_search
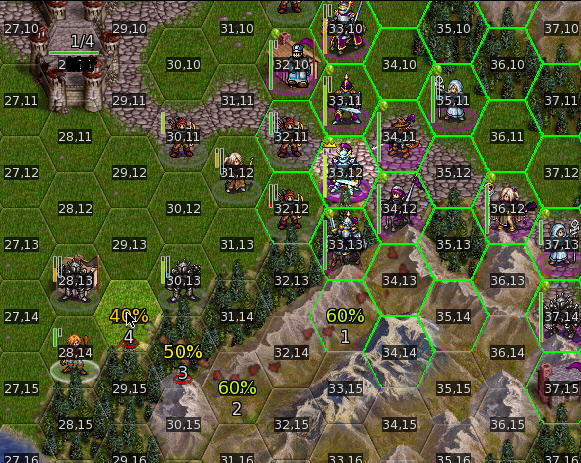
a_star_search找到一条从起点到终点路径。(shortest_path_calculator:消耗移动力最少)。下图的脚印指出一条路径(从(33,12)到(29,14))。
node中成员数据
- g:符合A*算法定义。指示起点到当前点路径代价。在值上差不多等于起点到当前点消耗移动力和,具体对应一路来cost之和。
- h:符合A*算法定义。指示当前点到终点路径代价。因为路径没有确定,只好用估值,heuristic函数执行这个估值。
- t:g+h。
a_star_search返回的plain_route内容
返回的plain_route指示了一条路径,就由两个变量组成。
- steps:一个std::vector<map_location>类型变量。其值就是从连缀出的从起到到终点路径。具体到示例图值是8个坐标,(33,12)(34,12)(34,13)(33,14)(32,14)(31,15)(30,14)(29.14).
- move_cost:steps这条路径消耗的移动力和。具体到示例图值是28。
@calc:对于当见情况,cost_calculator的原型是shortest_path_calculator,对应的cost也就是shortest_path_calculator::cost;pathfind::plain_route pathfind::a_star_search(const map_location& src, const map_location& dst,
double stop_at, const pathfind::cost_calculator *calc, const size_t width,
const size_t height, const std::set* teleports) {
//----------------- PRE_CONDITIONS ------------------
assert(src.valid(width, height));
assert(dst.valid(width, height));
assert(calc != NULL);
assert(stop_at <= calc->getNoPathValue());
//---------------------------------------------------
DBG_PF << "A* search: " << src << " -> " << dst << '\n';
// 对shortest_path_calculator,cost()返回值和src无关,值上大概等于单位在dst这格子上消耗的移动力,和dst是什么地形相关。
if (calc->cost(dst, 0) >= stop_at) {
LOG_PF << "aborted A* search because Start or Dest is invalid\n";
pathfind::plain_route locRoute;
locRoute.move_cost = int(calc->getNoPathValue());
return locRoute;
}
if (teleports && teleports->empty()) teleports = NULL;
std::vector locs(teleports ? 6 + teleports->size() : 6 );
if (teleports) {
std::copy(teleports->begin(), teleports->end(), locs.begin() + 6);
}
// increment search_counter but skip the range equivalent to uninitialized
search_counter += 2;
if (search_counter - bad_search_counter <= 1u)
search_counter += 2;
static std::vector nodes;
nodes.resize(width * height); // this create uninitalized nodes
indexer index(width, height);
comp node_comp(nodes);
nodes[index(dst)].g = stop_at + 1;
nodes[index(src)] = node(0, src, map_location::null_location, dst, true, teleports);
std::vector pq;
pq.push_back(index(src));
while (!pq.empty()) {
node& n = nodes[pq.front()];
n.in = search_counter;
std::pop_heap(pq.begin(), pq.end(), node_comp);
pq.pop_back();
if (n.t >= nodes[index(dst)].g) {
// 正常情况下,这里是退出while出口。随着枚举不断深入,dst会出现在某一次get_adjacent_tiles返回的格子中,到时nodes[index(dst)].g的值就会由初始设置的stop_at改到一个比stop_at小的值(大概等于选择了的src到dst这条路径上消耗移动力之和)
break;
}
get_adjacent_tiles(n.curr, &locs[0]);
int i = teleports && teleports->count(n.curr) ? locs.size() : 6;
for (; i-- > 0;) {
if (!locs[i].valid(width, height)) continue;
node& next = nodes[index(locs[i])];
// 如果next节点已被访问过,则门限值取next.g,否则取stop_at
double thresh = (next.in - search_counter <= 1u) ? next.g : stop_at + 1;
// cost() is always >= 1 (assumed and needed by the heuristic)
if (n.g + 1 >= thresh) continue;
// cost()返回值至少大于等于在locs[i]上的消耗移动力,移动力至少大于等于零
// 以下等式不是A*算法中的f(n) = g(n) + h(n),而是类似g(n + 1) = g(n-1) + g(n)
double cost = n.g + calc->cost(locs[i], n.g);
if (cost >= thresh) continue;
bool in_list = next.in == search_counter + 1;
next = node(cost, locs[i], n.curr, dst, true, teleports);
if (in_list) {
std::push_heap(pq.begin(), std::find(pq.begin(), pq.end(), index(locs[i])) + 1, node_comp);
} else {
pq.push_back(index(locs[i]));
std::push_heap(pq.begin(), pq.end(), node_comp);
}
}
}
pathfind::plain_route route;
if (nodes[index(dst)].g <= stop_at) {
DBG_PF << "found solution; calculating it...\n";
route.move_cost = static_cast(nodes[index(dst)].g);
for (node curr = nodes[index(dst)]; curr.prev != map_location::null_location; curr = nodes[index(curr.prev)]) {
route.steps.push_back(curr.curr);
}
route.steps.push_back(src);
std::reverse(route.steps.begin(), route.steps.end());
} else {
LOG_PF << "aborted a* search " << "\n";
route.move_cost = static_cast(calc->getNoPathValue());
}
return route;
}
五、其它
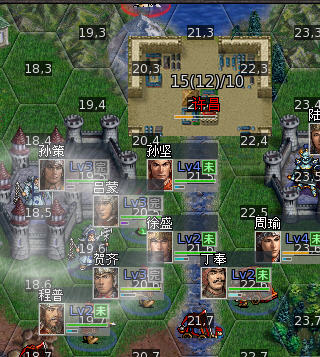
AI搜索空位,找到(19,4)。并形成路径(21,4)、(20,4)、(19,4)
但在实际出城时,(20, 5)站着孙坚,被zoc,出征立即结束,于是就看到不断有部队到(20,4)就回城情况。
这种情况会持续到另有一个部队以着另条路径把(19,4)给占掉。例如路径(21,4)、(20,3)、(19,4)。
以上过程形成路径用的是pathfind::a_star_search,使用的成本计算规则是pathfind::shortest_path_calculator;
出城用的是::move_unit;
结论
pathfind::shortest_path_calculator似乎把孙坚这个zoc给忽略了。