Ceres

《视觉SLAM十四讲(第二版)》中“6.3.2 使用Ceres进行曲线拟合”有介绍Ceres，本文不少内容抄自哪里。

Ceres是一个广泛使用的最小二乘问题求解库。在Ceres中，我们作为用户，只需按照一定步骤定义待解的优化问题，然后交给求解器计算。Ceres求解的最小二乘问题最一般的形式如下（带边界的核函数最小二乘）：

公式1： $\min_{x}\ \frac{1}{2}\sum_{i}^{}{\rho_{i}(\left|| f_{i}(x_{1},...,x_{k}) \right||^{2})}\ \ \ s.t.\ l_{j} \leq x_{j} \leq u_{j}$

我们的任务就是找到一组满足约束 $l_{j} \leq x_{j} \leq u_{j}$ 的 $x_{1},...,x_{k}$ ，使得优化目标函数 $\frac{1}{2}\sum_{i}^{}{\rho_{i}(\left|| f_{i}(x_{1},...,x_{k}) \right||^{2})}$ 取值最小。在Ceres库中，优化参数 $x_{1},...,x_{k}$ 被称为参数块(ParameterBlock)，它们的取值就是我们要寻找的解。 $l_{j},u_{j}$ 分别是第 $j$ 个优化参数 $x_{j}$ 的下界和上界。表达式 $\rho_{i}(\left|| f_{i}(x_{1},...,x_{k}) \right||^{2})$ 被称为残差项(ResidualBlock)。其中， $f_{i}\left( . \right)$ 是代价函数(CostFunction)， $\rho_{i}\left( . \right)$ 则是关于代价函数平方的核函数(LossFunction)。核函数存在的意义主要是为了降低野点(outliers)对于解的影响。

Ceres总逻辑

总体计算逻辑是一轮轮迭代。当此轮迭代的残差减去上一轮迭代的残差差值很小时（参考图1中的“absolute_function_tolerance”），认为迭代结束。结束判断条件是残差变化值，不是残差值。
如何计算此轮迭代残差。是Problem中，所有残差项(ResidualBlock)计算出的残差之“和”。“和”加引号，因为并不是简单相加。
如何计算残差项残差。一个残差项包含一个代价函数(CostFunction)，代价函数有一个输出项(成员函数operator()的最后一个参数)，它由我们算出传给ceres。
如何定义代价函数。operator()参数从左到右分为两类：输入参数和输出参数。输入指的是ceres面向应用，输出则相反。输入往往就是此次非线性优化要计算的最后结果，输出则是上一步所说用于存储残差。
对operator()输入、输出参数，它们类型是模板类型T，T实际类型是ceres::Jet。由于这些参数是ceres::Jet类型，一个标量要和它算术运算(加、减、乘、除等)时，须先转成ceres::Jet。转化方法是以标量为参数构造一个Jet对象。举个例子，x是一个double类型变量，它和输入、输出参数作算术运算时，须使用T(x)。
一次迭代中，某个代价函数虽然向Problem只AddResidualBlock了一次，但调用次数可能不只一次。是多次时，是调用所完代价函数后，再下一轮。正是这原因，CeresScanMatcher2D在执行优化时，在一次迭代，OccupiedSpaceCostFunction2D、TranslationDeltaCostFunctor2D、RotationDeltaCostFunctor2D极可能会先后执行两次。

一、使用Ceres

为使用Ceres求解问题，一般按以下步骤。

定义每个参数块。参数块通常为平凡的向量，但是在SLAM里也可以定义成四元数、李代数这种特殊的结构。如果是向量，那么需要为每个参数块分配一个double数组来存储变量的值。
定义残差项的计算方式。残差项通常关联若干个参数块，对它们进行一些自定义的计算，然后返回残差值。Ceres对它们求平方和之后，作为目标函数的值。
残差项往往也需要定义雅可比的计算方式。在Ceres中，你可以使用它提供的“自动求导”功能，也可以手动指定雅可比的计算过程。如果要使用自动求导，那么残差项需要按照特定的写法书写：残差的计算过程应该是一个带模板的operator()仿函数。
把所有的参数块和残差项加入Ceres对象中，调用Solve函数即可。求解之前，我们可以传入一些配置信息，例如迭代次数、终止条件等，也可以使用默认配置。

作为演示代码，这里使用《视觉SLAM十四讲(第二版)》中曲线拟合示例。

struct CURVE_FITTING_COST 
{
    CURVE_FITTING_COST(double x, double y)
        : _x(x)
        , _y(y)
    {}

    template<typename T>
    bool operator()(const T* const abc, T* residual) const
    {
        // y - exp(ax^2 + bx + c)
        residual[0] = T(_y) - ceres::exp(abc[0] * T(_x) * T(_x) + abc[1] * T(_x) + abc[2]);
        return true;
    }

CURVE_FITTING_COST必须实现仿函数operator()，注意函数带const修饰符。它将作为此残差项的代价函数。abc是输入参数。residual是输出参数，存储代价函数计算出的残差值。代价函数中，模块参数T的真实类型是ceres::Jet。由于abc、residual是ceres::Jet类型，一个标量要和它算术运算(加、减、乘、除等)时，须先转成ceres::Jet。转化方法是以标量为参数构造一个Jet对象。举个例子，_x是一个double类型变量，它和输入、输出参数作算术运算时，须使用T(_x)。

    double _x;
    double _y;
};

void test_slam()
{
    double ar = 1.0, br = 2.0, cr = 1.0; // real value
    double ae = 2.0, be = -1.0, ce = 5.0; // estimate value
    int N = 100;
    double w_sigma = 1.0;
    double inv_sigma = 1.0 / w_sigma;
    cv::RNG rng;

    std::vector<double> x_data, y_data;
    for (int i = 0; i < N; i ++) {
        double x = i / 100.0;
        x_data.push_back(x);
        y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(w_sigma * w_sigma));
    }

给定一条满足以下方程的曲线：

$y=exp(ax^{2}+bx+c)$

其中a、b、c为曲线参数，w_sigma为高斯噪声，满足 $w\_sigma\sim(0,\sigma^{2})$ 。现在假设我们有N个关于x、y的观测点，想根据这些数据求出曲线的参数。请注意，在这个问题中，待估计变量是a、b、c，而不是x。以上for循环先根据模型生成x、y的真值，然后在真值中添加高斯分布的噪声。

    double abc[3] = {ae, be, ce};

步骤1：定义参数块。参数块是平凡向量，需要为每个参数块分配一个double数组来存储变量的值。

    ceres::Problem problem;
    for (int i = 0; i < N; i ++) {
        problem.AddResidualBlock(
            new ceres::AutoDiffCostFunction<CURVE_FITTING_COST, 1, 3>(
                new CURVE_FITTING_COST(x_data[i], y_data[i])),
            nullptr,
            abc
        );

步骤2、3：定义一次迭代中有哪些残差项，以及它们的的计算方式，并加入Problem。在此个应用中，一次迭代包含N个参残项，这N个残差项虽然有着类似的代价函数，但它们的确是不同的残差项。

在AddResidualBlock将残差项添加到目标函数时，由于优化需要梯度，这里有三种选择。1）使用Ceres自动求导(Auto Diff)。2）使用数值求导(Numeric Diff)。3）自行推导解析的导数形式，提供给Ceres。这里使用第一种。自动求导需要指定残差项和参数块的维度。这里的残差是标量，维度为1；参数块(待优化)是a、b、c三个量，维度3。于是在自动求导类AutoDiffCostFunction的模板参数中设定变量维度为1、3。

    }

    ceres::Solver::Options options;
    options.linear_solver_type = ceres::DENSE_NORMAL_CHOLESKY;
    options.minimizer_progress_to_stdout = true;

    ceres::Solver::Summary summary;
    uint32_t t1 = SDL_GetTicks();
    ceres::Solve(options, &problem, &summary);

步骤4：调用ceres::Solve执行优化。

    uint32_t t2 = SDL_GetTicks();

    std::stringstream ss;
    ss << "message: " << summary.message.c_str() << "\n";
    ss << "solve time cost = " << (t2 - t1) << " ms. ";
    ss << "estimated a, b, c = ";
    for (auto a: abc) ss << a << " ";
    SDL_Log("%s", ss.str().c_str());
}

以下是过程中输出log。

iter      cost      cost_change  |gradient|   |step|    tr_ratio  tr_radius  ls_iter  iter_time  total_time
   0  1.597873e+06    0.00e+00    3.52e+06   0.00e+00   0.00e+00  1.00e+04        0    1.42e-03    1.77e-03
   1  1.884440e+05    1.41e+06    4.86e+05   9.88e-01   8.82e-01  1.81e+04        1    1.42e-03    3.37e-03
   2  1.784821e+04    1.71e+05    6.78e+04   9.89e-01   9.06e-01  3.87e+04        1    1.10e-03    4.59e-03
   3  1.099631e+03    1.67e+04    8.58e+03   1.10e+00   9.41e-01  1.16e+05        1    1.03e-03    5.72e-03
   4  8.784938e+01    1.01e+03    6.53e+02   1.51e+00   9.67e-01  3.48e+05        1    1.04e-03    6.85e-03
   5  5.141230e+01    3.64e+01    2.72e+01   1.13e+00   9.90e-01  1.05e+06        1    1.04e-03    7.99e-03
   6  5.096862e+01    4.44e-01    4.27e-01   1.89e-01   9.98e-01  3.14e+06        1    1.04e-03    9.16e-03
   7  5.096851e+01    1.10e-04    9.53e-04   2.84e-03   9.99e-01  9.41e+06        1    1.08e-03    1.03e-02
message: Function tolerance reached. |cost_change|/cost: 1.086533e-11 <= 1.000000e-06
solve time cost = 11 ms. estimated a, b, c = 0.890908 2.1719 0.943628

Ceres更多使用实例参考“Ceres入门——Ceres的基本使用方法”。

二、迭代结束条件：FunctionToleranceReached

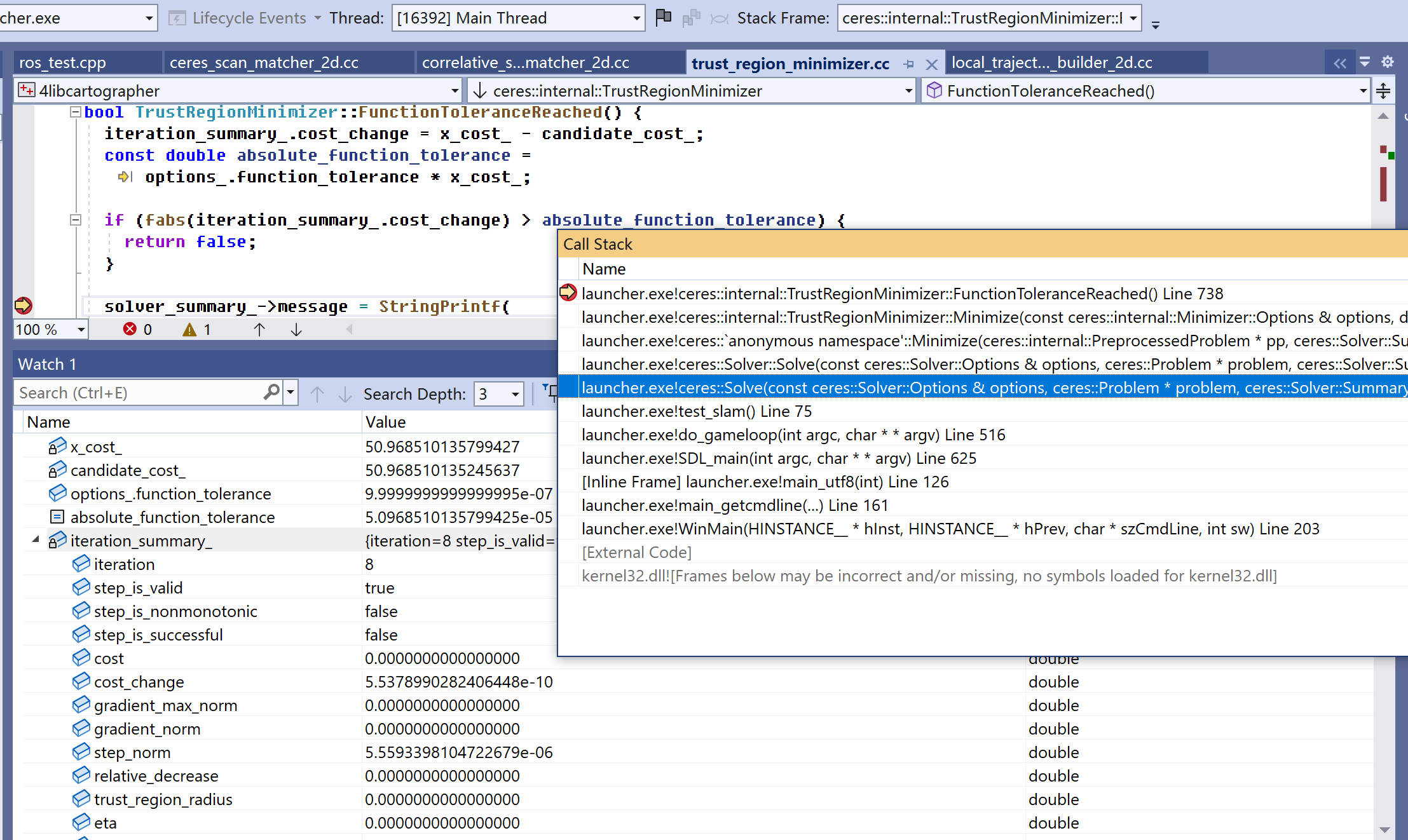
bool TrustRegionMinimizer::FunctionToleranceReached() {
  iteration_summary_.cost_change = x_cost_ - candidate_cost_;
  const double absolute_function_tolerance =
      options_.function_tolerance * x_cost_;

  if (fabs(iteration_summary_.cost_change) > absolute_function_tolerance) {
    return false;
  }

x_cost_。上一轮迭代计算出的不包含solver_summary_->fixed_cost的cost。对照看上面“过程中输出log”和图1，因为fixed_cost是0，x_cost_就是log中第7轮迭代的cost。
candidate_cost_。此轮迭代计算出的不包含solver_summary_->fixed_cost的cost。
iteration_summary_.cost_change。此轮迭代的cost变化量。
options_.function_tolerance。(new_cost - old_cost) < function_tolerance * old_cost。默认值：1e-6。

  solver_summary_->message = StringPrintf(
      "Function tolerance reached. "
      "|cost_change|/cost: %e <= %e",
      fabs(iteration_summary_.cost_change) / x_cost_,
      options_.function_tolerance);
  solver_summary_->termination_type = CONVERGENCE;
  if (is_not_silent_) {
    VLOG(1) << "Terminating: " << solver_summary_->message;
  }
  return true;
}

三、log输出到Windows

minimizer_progress_to_stdout为true时，表示要输出log。log的目的地是控制台，具体在win10，输出到Console。但在win10用的Subsystem是Windows，为输出到Windows，须要修改log输出函数。

<ceres>/internal/ceres/callbacks.cc
------
CallbackReturnType LoggingCallback::operator()(
    const IterationSummary& summary) {
  ...
  if (log_to_stdout_) {
    // std::cout << output << std::endl;
    // 改为用SDL_Log。output是log内容。
    SDL_Log("%s", output.c_str());
  } else {
    VLOG(1) << output;
  }
  return SOLVER_CONTINUE;
}

全部评论: 0 条