后端优化问题求解器——optimization_problem_
- 每一轮迭代时残差项至少有两种,constraints.size()个node和子图之间约束生成的残差项,和“node_data_.size()-1”个相邻节点生成的残差项。
一、SPA 优化问题建模
SPA(Sparse Pose Adjustment)优化是一种位姿图优化技术(Pose Graph),其优化的对象是所有节点的世界位姿(base_footprint到/map的tf)。在一些视觉SLAM方案中,节点由视觉关键帧组成,我们根据前端里程计在关键帧之间构建相对位姿约束 —— 边,如经典的 ORB-SLAM。
Cartographer在后端(Global SLAM)使用SPA优化。节点共有两类 —— 点云节点和子图节点,点云指的是激光雷达点云,而子图(submap)是由连续的若干个雷达点云拼接到一起形成的子地图。这两类节点都是我们的优化对象,所有的约束(边)都是在这两类节点之间构建,同类节点之间不构建约束(我们暂且这么认为,实际Cartographer中稍有不同),如图1所示。
下文中,子图节点简称为submap,点云节点简称为node,两者统称为节点。这种叫法是为了与Cartographer保持一致,请不要混淆 node 与 节点 这两个概念。
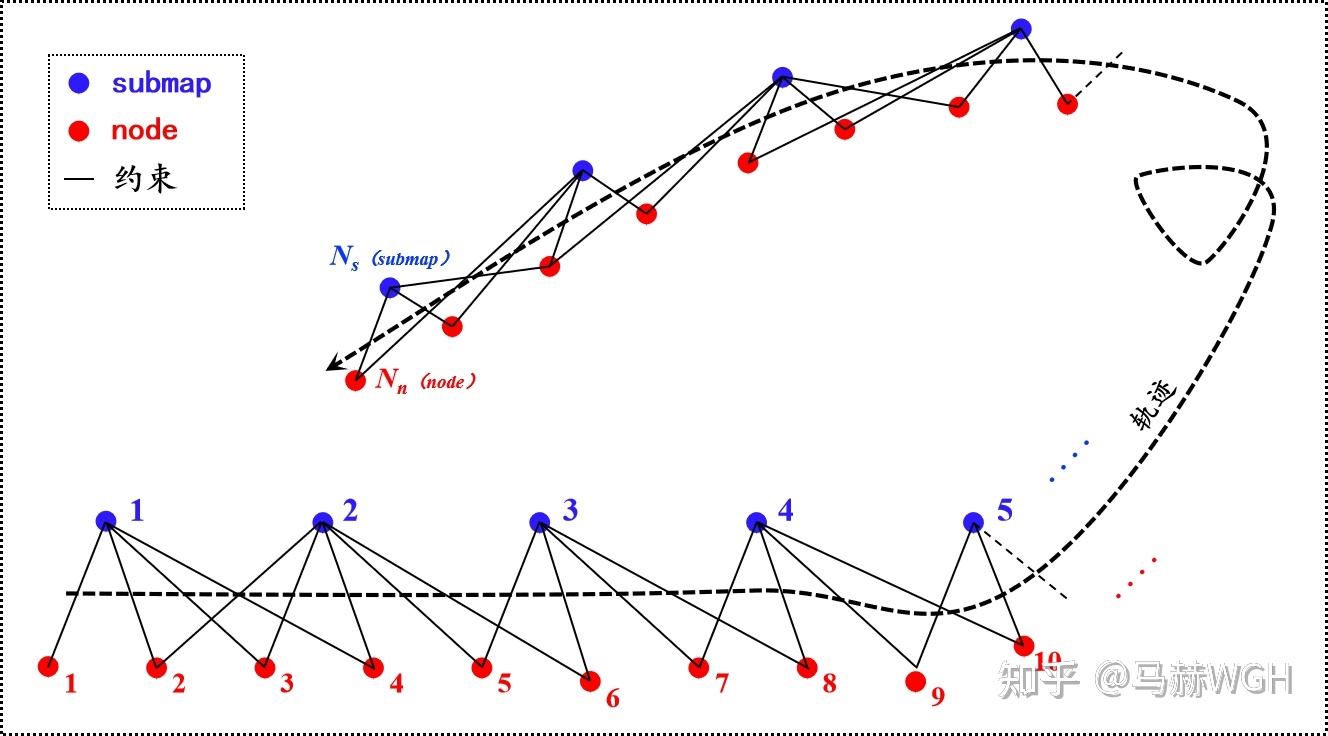
** 以下两段文字非必须,读者可跳过~ **
顺便提一下Carto中约束的构建过程:每一个雷达点云都会在前端中与1个子图进行 scan-to-submap 配准,得到一个相对位姿,关键帧按照此相对位姿插入到最新的2个子图中,并与这2个子图分别构建约束(称为 intra constraint);而对于更早的子图(标记为 finished 状态),关键帧会在后端中与它们逐一尝试配准,如果配准得分足够高,就按配准位姿在两者之间构建约束(此类约束称为 inter constraint),这个发生在后端中的配准,正是Carto的回环检测。值得注意的是,当前端中的子图插入了一定数量的关键帧后,就会变成 finished 状态,当一个子图刚刚变为 finished 状态时,我们称之为 "newly finished submap",这种 "newly finished submap" 会反过来去跟所有过去的关键帧尝试配准(该过程也发生在后端中,实际上还是回环检测),如果配准成功就同样构建一项 inter constraint。(注:"newly finished submap" 完成此次反向搜索之后就变成了普通的“更早的子图”中的一员) 这样,就形成了 关键帧 和 子图 之间的双向搜索。这样密集的双向搜索必然会形成过多的约束,破坏稀疏性,但不搜索的话就没法形成回环约束,于是 Carto 设置了搜索采样率,来兼顾两者。
不知不觉扯了一大段,...... ,实际上 Carto 后端约束构建逻辑还要更复杂(精巧)一点,比如跨轨迹的约束构建,也正是借助跨轨迹约束构建,Carto 实现了地图拼接,multi-robots mapping 等功能,关于 Carto后端约束构建逻辑的完整阐述 —— 还是有时间再说吧 ......
其实如果不发生回环的话,就没有必要优化了。如 图2 所示,回环的作用在于告诉你,你的累积误差(drift)有多大。而优化的任务在于,把这个累积的误差,分摊到所有的节点之间,以使得总体的误差最小化,为此,我们首先明确一下误差项的概念。
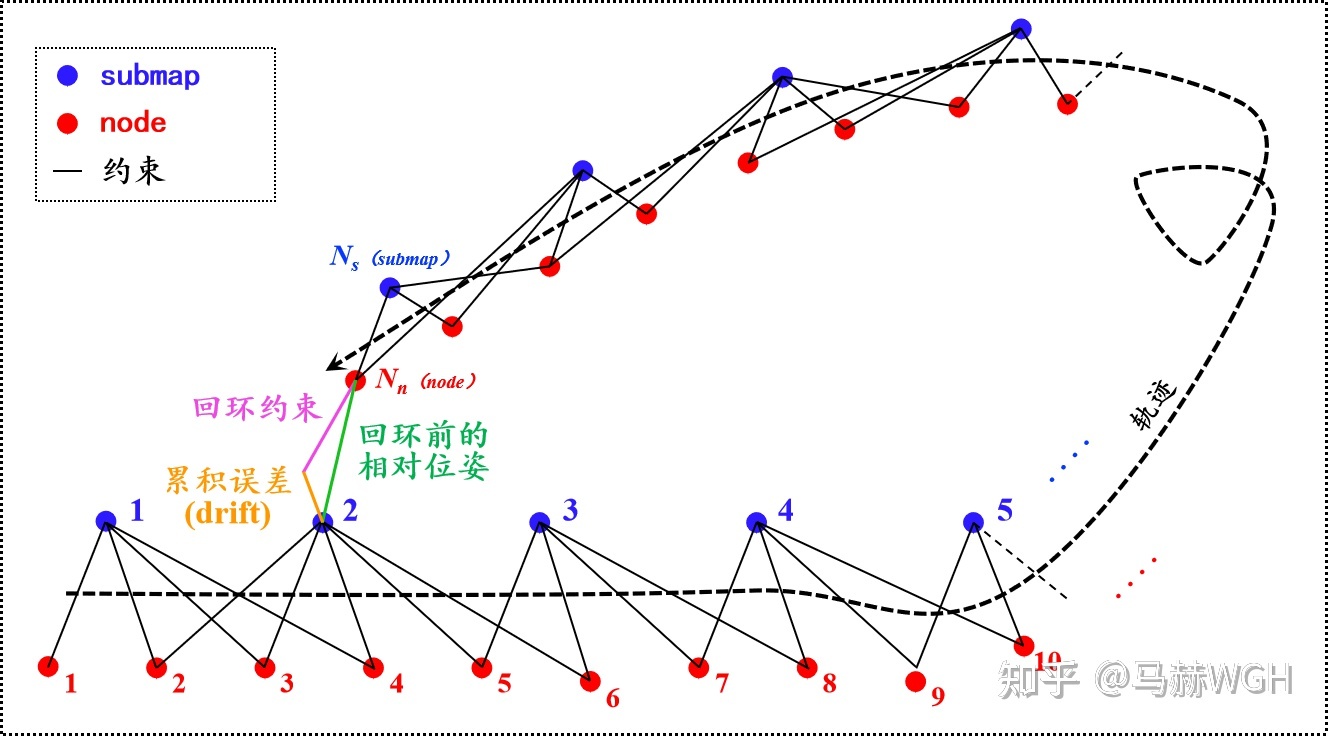
误差项衡量的是观测值和“真值”之间的误差,一个约束唯一构建一个误差项,以第 i 个submap和第 j 个node为例,它们之间的约束是相对位姿观测值,该相对位姿在submap坐标系下表示。对应的误差项表示为:
其中 分别代表submap和node的世界位姿,是变量;
表示第 j 个node 在第 i 个 submap 中的坐标,
代表的就是坐标转换关系。优化时,
和
作为优化变量存在,在优化中不断逼近“真值”,而
作为常量参数存在;不难发现,
代表的就是观测值和“真值”之间的误差,由于我们相信观测值是局部准确的,因此 作用就相当于“弹簧”一样牵拉着
和
,约束着它们在优化过程中不被调整的太多,这也正是“约束”一词的含义。
更形象一点,你可以把整个位姿图想象成一个节点和弹簧(约束)组成的能量系统,优化的过程就是让真个能量系统蕴含的能量最小化!弹簧在不同方向上的刚度不一样,代表着不同方向的权重。
假设我们共有个误差项,我们的优化目标是 —— 让所有
个误差项的总体误差最小。
二、OptimizationProblem2D::Solve
<cartographer>/cartographer/mapping/internal/optimization/optimization_problem_2d.cc
------
void OptimizationProblem2D::Solve(
const std::vector<Constraint>& constraints,
const std::map<int, PoseGraphInterface::TrajectoryState>&
trajectories_state,
const std::map<std::string, LandmarkNode>& landmark_nodes) {
if (node_data_.empty()) {
// Nothing to optimize.
return;
}
std::set<int> frozen_trajectories;
for (const auto& it : trajectories_state) {
if (it.second == PoseGraphInterface::TrajectoryState::FROZEN) {
frozen_trajectories.insert(it.first);
}
}
ceres::Problem::Options problem_options;
ceres::Problem problem(problem_options);
// Set the starting point.
// TODO(hrapp): Move ceres data into SubmapSpec.
MapById<SubmapId, std::array<double, 3>> C_submaps;
MapById<NodeId, std::array<double, 3>> C_nodes;
std::map<std::string, CeresPose> C_landmarks;
bool first_submap = true;根据Ceres库的使用套路,先创建优化问题对象。同时创建了一些临时的变量,用于描述优化问题。
for (const auto& submap_id_data : submap_data_) {
const bool frozen =
frozen_trajectories.count(submap_id_data.id.trajectory_id) != 0;
C_submaps.Insert(submap_id_data.id,
FromPose(submap_id_data.data.global_pose));
problem.AddParameterBlock(C_submaps.at(submap_id_data.id).data(), 3);
if (first_submap || frozen) {
first_submap = false;
// Fix the pose of the first submap or all submaps of a frozen
// trajectory.
problem.SetParameterBlockConstant(C_submaps.at(submap_id_data.id).data());
}
}在一个for循环中,我们遍历所有的子图,将子图的全局位姿放置到刚刚构建的临时容器C_submaps中,并通过AddParameterBlock显式的将子图全局位姿作为优化参数告知对象problem。 如果是第一幅子图,或者已经冻结了,就通过SetParameterBlockConstant将对应的参数设定为常量,那么Ceres在迭代求解的过程中将不会改变这些参数。
for (const auto& node_id_data : node_data_) {
const bool frozen =
frozen_trajectories.count(node_id_data.id.trajectory_id) != 0;
C_nodes.Insert(node_id_data.id, FromPose(node_id_data.data.global_pose_2d));
problem.AddParameterBlock(C_nodes.at(node_id_data.id).data(), 3);
if (frozen) {
problem.SetParameterBlockConstant(C_nodes.at(node_id_data.id).data());
}
}同样的遍历所有的路径节点,将他们的全局位姿作为优化参数告知对象problem。如果该节点所在的路径被冻结了,就将它所对应的优化参数设为常量。
// Add cost functions for intra- and inter-submap constraints.
for (const Constraint& constraint : constraints) {
problem.AddResidualBlock(
CreateAutoDiffSpaCostFunction(constraint.pose),
// Loop closure constraints should have a loss function.
constraint.tag == Constraint::INTER_SUBMAP
? new ceres::HuberLoss(options_.huber_scale())
: nullptr,
C_submaps.at(constraint.submap_id).data(),
C_nodes.at(constraint.node_id).data());
}紧接着就是遍历所有的约束,描述优化问题的残差块。函数CreateAutoDiffSpaCostFunction用于提供对应约束的SPA代价计算。如果是通过闭环检测构建的约束,则为之提供一个Huber的核函数, 用于降低错误的闭环检测对最终的优化结果带来的负面影响。
// Add cost functions for landmarks. AddLandmarkCostFunctions(landmark_nodes, node_data_, &C_nodes, &C_landmarks, &problem, options_.huber_scale());
然后调用成员函数AddLandmarkCostFunctions,根据路标点添加残差项。并且遍历所有的路径节点,根据Local SLAM以及里程计等局部定位的信息建立相邻的路径节点之间的位姿变换关系。 并将之描述为残差项提供给problem对象。
// Add penalties for violating odometry or changes between consecutive nodes
// if odometry is not available.
for (auto node_it = node_data_.begin(); node_it != node_data_.end();) {
const int trajectory_id = node_it->id.trajectory_id;
const auto trajectory_end = node_data_.EndOfTrajectory(trajectory_id);
if (frozen_trajectories.count(trajectory_id) != 0) {
node_it = trajectory_end;
continue;
}
auto prev_node_it = node_it;
for (++node_it; node_it != trajectory_end; ++node_it) {
const NodeId first_node_id = prev_node_it->id;
const NodeSpec2D& first_node_data = prev_node_it->data;
prev_node_it = node_it;
const NodeId second_node_id = node_it->id;
const NodeSpec2D& second_node_data = node_it->data;
if (second_node_id.node_index != first_node_id.node_index + 1) {
continue;
}
// Add a relative pose constraint based on the odometry (if available).
std::unique_ptr<transform::Rigid3d> relative_odometry =
CalculateOdometryBetweenNodes(trajectory_id, first_node_data,
second_node_data);
if (relative_odometry != nullptr) {
problem.AddResidualBlock(
CreateAutoDiffSpaCostFunction(Constraint::Pose{
*relative_odometry, options_.odometry_translation_weight(),
options_.odometry_rotation_weight()}),
nullptr /* loss function */, C_nodes.at(first_node_id).data(),
C_nodes.at(second_node_id).data());这里有个problem.AddResidualBlock,但对rose_ros来说,relative_odometry总是nullptr,不会添加这里的残差项。
}
// Add a relative pose constraint based on consecutive local SLAM poses.
const transform::Rigid3d relative_local_slam_pose =
transform::Embed3D(first_node_data.local_pose_2d.inverse() *
second_node_data.local_pose_2d);
problem.AddResidualBlock(
CreateAutoDiffSpaCostFunction(
Constraint::Pose{relative_local_slam_pose,
options_.local_slam_pose_translation_weight(),
options_.local_slam_pose_rotation_weight()}),
nullptr /* loss function */, C_nodes.at(first_node_id).data(),
C_nodes.at(second_node_id).data());这段代码主要是给相邻路径节点之间添加约束。[first_node_id(0, 0) second_node_id(0, 1)]、[(0, 1), (0, 2)],依此类推,此处会增加“node_data_.size()-1”个残差项。
}
}
std::map<int, std::array<double, 3>> C_fixed_frames;
for (auto node_it = node_data_.begin(); node_it != node_data_.end();) {
const int trajectory_id = node_it->id.trajectory_id;
const auto trajectory_end = node_data_.EndOfTrajectory(trajectory_id);
if (!fixed_frame_pose_data_.HasTrajectory(trajectory_id)) {
node_it = trajectory_end;
continue;这个for内有个problem.AddResidualBlock,但对rose_ros来说,fixed_frame_pose_data_总是空,进入这个if块continue,不会添加这里的残差项。
}
...
}
}
// Solve.
ceres::Solver::Summary summary;
ceres::Solve(
common::CreateCeresSolverOptions(options_.ceres_solver_options()),
&problem, &summary);
if (options_.log_solver_summary()) {
LOG(INFO) << summary.FullReport();
}在描述完优化参数和残差计算方式之后,我们就可以通过ceres求解优化问题。局部对象summary将记录整个求解过程。
// Store the result.
for (const auto& C_submap_id_data : C_submaps) {
submap_data_.at(C_submap_id_data.id).global_pose =
ToPose(C_submap_id_data.data);
}
for (const auto& C_node_id_data : C_nodes) {
node_data_.at(C_node_id_data.id).global_pose_2d =
ToPose(C_node_id_data.data);
}
for (const auto& C_fixed_frame : C_fixed_frames) {
trajectory_data_.at(C_fixed_frame.first).fixed_frame_origin_in_map =
transform::Embed3D(ToPose(C_fixed_frame.second));
}
for (const auto& C_landmark : C_landmarks) {
landmark_data_[C_landmark.first] = C_landmark.second.ToRigid();
}最后记录下优化结果。
}
三、CreateAutoDiffSpaCostFunction、SpaCostFunction2D
ceres::CostFunction* CreateAutoDiffSpaCostFunction(
const PoseGraphInterface::Constraint::Pose& observed_relative_pose) {
return new ceres::AutoDiffCostFunction<SpaCostFunction2D, 3 /* residuals */,
3 /* start pose variables */,
3 /* end pose variables */>(
new SpaCostFunction2D(observed_relative_pose));
}不论是由约束生成,还是两相邻node生成的残差项,用的代价函数都是SpaCostFunction2D::operator()。
<cartographer>/cartographer/mapping/internal/optimization/cost_functions/spa_cost_function_2d.cc
------
class SpaCostFunction2D {
public:
explicit SpaCostFunction2D(
const PoseGraphInterface::Constraint::Pose& observed_relative_pose)
: observed_relative_pose_(observed_relative_pose) {}
template <typename T>
bool operator()(const T* const start_pose, const T* const end_pose,
T* e) const {
const std::array<T, 3> error =
ScaleError(ComputeUnscaledError(
transform::Project2D(observed_relative_pose_.zbar_ij),
start_pose, end_pose),
observed_relative_pose_.translation_weight,
observed_relative_pose_.rotation_weight);
std::copy(std::begin(error), std::end(error), e);
return true;
}
private:
const PoseGraphInterface::Constraint::Pose observed_relative_pose_;
};
3.2 ComputeUnscaledError
/**
* @brief 2d 根据SPA论文里的公式求残差
*
* 计算残差:
* T12 = T1.inverse() * T2
* [R1.inverse * R2, R1.inverse * (t2 -t1)]
* [0 , 1 ]
*
* @param[in] relative_pose
* @param[in] start
* @param[in] end
* @return std::array<T, 3>
* 这里 relative_pose 为论文中的计算值 zij start与end的实际值offset 为h(ci,cj)
*
* 根据论文计算公式是这样的,先把角度theta(start位姿的theta)转换为2*2的旋转矩阵R [ cos(theta) -sin(theta)
* sin(theta) cos(theta) ]
* 再对R取转置 RT [ cos(theta) sin(theta)
* -sin(theta) cos(theta) ]
* ci,cj的 h(ci,cj) = { RT(tj-ti)
* theta(j)-theta(i)
* }
* 所以RT(tj-ti) = [cos(theta) sin(theta)
* -sin(theta) cos(theta) ] [ deltax deltay]
*
*下面的h3就是这么算的
*
*
* eij = zij - h(ci,cj)
* 不明白的地方去看 Efficient Sparse Pose Adjustment for 2D Mapping 这个论文
*/
<cartographer>/cartographer/mapping/internal/optimization/cost_functions/cost_helpers_impl.h
------
template <typename T>
static std::array<T, 3> ComputeUnscaledError(
const transform::Rigid2d& relative_pose, const T* const start,
const T* const end) {
const T cos_theta_i = cos(start[2]);
const T sin_theta_i = sin(start[2]);
const T delta_x = end[0] - start[0];
const T delta_y = end[1] - start[1];
const T h[3] = {cos_theta_i * delta_x + sin_theta_i * delta_y,
-sin_theta_i * delta_x + cos_theta_i * delta_y,
end[2] - start[2]};
return {{T(relative_pose.translation().x()) - h[0],
T(relative_pose.translation().y()) - h[1],
common::NormalizeAngleDifference(
T(relative_pose.rotation().angle()) - h[2])}};
}ComputeUnscaledError结束后,返回值是一个3单元数组,分别是误差的x、y和theta。
3.3 ScaleError
2d时,为残差中的x、y与theta分别乘上不同的权重
<cartographer>/cartographer/mapping/internal/optimization/cost_functions/cost_helpers_impl.h
------
template <typename T>
std::array<T, 3> ScaleError(const std::array<T, 3>& error,
double translation_weight, double rotation_weight) {
// clang-format off
return {{
error[0] * translation_weight,
error[1] * translation_weight,
error[2] * rotation_weight
}};
// clang-format on
}ComputeUnscaledError结束后,返回值是一个3单元数组,分别是乘上权重的误差的x、y和theta。