probability_values.h/c：占据概率相关

此文第一、第二节抄自“Cartographer源码阅读之附 1—probability_values.h/c：占据概率相关^[1] ”

在概率上，要解决一个问题：对于这个cell，新来了一个测量值——即传感器测得该点为occupied或Free，我们如何根据该测量值来更新该点的状态呢？——在cartographer，是用CorrespondenceCostValue（整数表示的空闲概率）表示栅格状态，换句话说：对于这个cell，新来了一个测量值——即传感器测得该点为occupied或Free，我们如何根据该测量值来更新该点的CorrespondenceCostValue呢？

解决这问题，cardtographer用了两张查找表：hit_table_、miss_table_。这两张表也称概率更新表，概率更新表存储着更新后的值，而对应该行的索引就是更新前的值。至于构建表的方法是ComputeLookupTableToApplyCorrespondenceCostOdds。

hit_table_解决新来测量值是occupied时，如何更新该点的CorrespondenceCostValue。
miss_table_解决新来测量值是free时，如何更新该点的CorrespondenceCostValue。

一、占据栅格图(Occupancy Grid Map)更新公式推导

编程我不擅长，但推公式我很擅长，所以我就把这块儿的公式讲解一下吧，也都是很基础的内容。

对于栅格化地图中的一个cell, 或者说一个pixel，它的状态 $s$ 可能有两个状态：

$s = 1$ : 表示该点被occupied的

$s = 0$ : 表示该点是Free的

通常，我们用一个概率 $p(s=1)$ 来表示该pixel被占据(occupied)的概率。那么，该点Free的概率就是 $p(s=0) = 1 - p(s = 1)$ 。

但是，对于同一个点用两个值表达比较麻烦，而且也不便于概率值的更新。所以，这里会引入一个新的变量Odd(s)——用两个概率的比值表示：

$Odd(s) = \frac{p(s=1)}{p(s=0)}$

odds表示occupied概率与free概率的比值。

Odd(s)值等于1时，表征一半对一半，该点被occupied和free的概率各为0.5。
如果Odd(s)值大于1，表征该点被occupied的概率更大；Odd(s)越大，occupied的概率越大。范围为1～+ $\infty$ 。
如果Odd(s)值小于1，表征该点free的概率更大；Odd(s)越小，free的概率越大。范围为0~1。

那么对于这个cell，新来了一个测量值 $z$ ——即传感器测得该点为occupied或Free，我们如何根据该测量值来更新该点的状态呢？

分为两种情况讨论：

Case 1：假设之前我们对该点没有任何信息，那么我们会直接把测量值赋给该点：

$p(s=1) = z(s=1)$

$odd(s) = \frac{p(s=1)}{p(s=0)}$

Case 2: 假设测量值来之前，该点已有一个测量值odd(s).

我们要求的实际上是一个条件概率：

$odd(s|z) = \frac{p(s=1|z)}{p(s=0|z)}$

即，在存在观测值 $z$ 的条件下，该点的实际状态为 $s=1$ 的概率与该点的实际状态为 $s=0$ 的比值。

那么，根据贝叶斯的条件概率公式，我们有：

$p(s=1|z)=\frac{p(z|s=1)p(s=1)}{p(z)}$

$p(s=0|z)=\frac{p(z|s=0)p(s=0)}{p(z)}$

所以，我们可以得到：

$odd(s|z)=\frac{p(z|s=1)p(s=1)}{p(z|s=0)p(s=0)}=\frac{p(z|s=1)}{p(z|s=0)}.\frac{p(s=1)}{p(s=0)}$

其中， $\frac{p(s=1)}{p(s=0)}$ 即为上一次的状态，即odd(s). 所以，我们可以得到更新模型为：

$odd(s|z)=\frac{p(z|s=1)}{p(z|s=0)}odd(s)$

其中， $\frac{p(z|s=1)}{p(z|s=0)}$ 表征的是传感器的测量模型。 $p(z|s=1)$ 的含义是在实际状态为occupied的条件下，测量结果是 $z$ 的概率。同样， $p(z|s=0)$ 的含义是在实际状态为free的条件下，测量结果是 $z$ 的概率。这两个值是由传感器的测量精度、可靠性等因素决定。当一个传感器制造完成后，该值是定值，不会随时间、位置等因素改变(当然，如果你的传感器是随着时间、位置等因素而变化的，这不在我们讨论范围内，你需要一个新的传感器模型）。

为了更方便计算，可以对两边取log，可以得到：

$log(odd(s|z))=log(\frac{p(z|s=1)}{p(z|s=0)})+log(odd(s))$

那么，根据测量结果z是occupied或free的情况，我们可以预先求出来两个值：

$S_{free}=log(\frac{p(z=0|s=1)}{p(z=0|s=0)})$

$S_{occupied}=log(\frac{p(z=1|s=1)}{p(z=1|s=0)})$

则：

$S_z =\log \frac{p(z|s=1)}{p(z|s=0)} = \left\{ \begin{array}{*{20}{l}} S_{free}&z = 0 \\ S_{occupied} &z=1\end{array} \right.\\$

记：

$S^{+}=odd(s|z), S^{-}=odd(s)$

则我们的更新模型就可以得到:

$S^{+} = S^{-}+S_{z}$

这个就是我们在占据概率图里通常使用的更新模型。

二、probability_values.h/.cc解读

可以看到，在前面公式推导中，有三个变量我们需要经常遇到：被占据的概率 $p(s=1)$ 、Free的概率 $p(s=0)$ 和两者的比值odd(s).

在cartographer的源码里，也必然涉及到很多对这三个量的相互转化以及模型更新等公式的计算。这部分工作是在/mapping/probability_values.h/.cc中完成的。我们来看看这部分代码：

cartographer中 $p(s=1)$ 称为Probability，后面公式中我用 $p$ 表示；

$p(s=0)$ 称为CorrespondenceCost，后面公式中我用 $c$ 表示

Odd(s)记为了Odds。

首先，在/mapping/probability_values.h里定义了几个常量：

constexpr float kMinProbability = 0.1f; //最小Occupied概率为0.1
constexpr float kMaxProbability = 1.f - kMinProbability; //最大Occupied概率为1-0.1=0.9
constexpr float kMinCorrespondenceCost = 1.f - kMaxProbability; //最小Free概率
constexpr float kMaxCorrespondenceCost = 1.f - kMinProbability; //最大Free概率

以及：

//在没有任何先验信息情况下，Occupied和Free概率值都为0
constexpr uint16 kUnknownProbabilityValue = 0;
constexpr uint16 kUnknownCorrespondenceValue = kUnknownProbabilityValue;
// 非常抱歉，之前我把左移看成了右移，所以认为kUpdateMarker是一个极小值，所以导致大家对代码的理解出现了问题。
// 左移的话kUpdateMarker是2的15次方：32768，也就是所以概率值转化成整数value之后的最大范围。所以程序中有判断是否越界
constexpr uint16 kUpdateMarker = 1u << 15;

首先提供了如下转化工具：

//由Probability计算odds
inline float Odds(float probability) {
  return probability / (1.f - probability);
}

$odds=\frac{p}{1-p}$

//由odds计算probability
inline float ProbabilityFromOdds(const float odds) {
  return odds / (odds + 1.f);
}

根据之前的公式，容易推得：

$p=\frac{odds}{odds+1}$

//Probability转CorrespondenceCost
inline float ProbabilityToCorrespondenceCost(const float probability) {
  return 1.f - probability;
}

$c=1-p$

// CorrespondenceCost转Probability
inline float CorrespondenceCostToProbability(const float correspondence_cost) {
  return 1.f - correspondence_cost;
}

$p=1-c$

两个Clamp函数：

// Clamps probability to be in the range [kMinProbability, kMaxProbability].
// clamp函数的含义是，如果给定参数小于最小值，则返回最小值；如果大于最大值则返回最大值；其他情况正常返回参数
inline float ClampProbability(const float probability) {
  return common::Clamp(probability, kMinProbability, kMaxProbability);
}
// Clamps correspondece cost to be in the range [kMinCorrespondenceCost,
// kMaxCorrespondenceCost].
inline float ClampCorrespondenceCost(const float correspondence_cost) {
  return common::Clamp(correspondence_cost, kMinCorrespondenceCost,
                       kMaxCorrespondenceCost);
}

cartongrapher为了尽量避免浮点运算，将[kMinProbability, kMaxProbability]或[kMinCorrespondenceCost, kMaxCorrespondenceCost]之间的浮点数映射到了整数区间：[1, 32767]:

由浮点数到整数区间的映射函数为：

inline uint16 BoundedFloatToValue(const float float_value,
                                  const float lower_bound,
                                  const float upper_bound) {
  const int value =
      common::RoundToInt(
          (common::Clamp(float_value, lower_bound, upper_bound) - lower_bound) *
          (32766.f / (upper_bound - lower_bound))) +
      1;
  // DCHECK for performance.
  DCHECK_GE(value, 1);//检查是否大于等于1
  DCHECK_LE(value, 32767);//是否小于等于32767
  return value;
}

$f(x)=(clamp(x,min,max)-min)\frac{32766}{max-min}+1$

Probability和CorrespondenceCost向整数区间映射：

// Converts a probability to a uint16 in the [1, 32767] range.
inline uint16 ProbabilityToValue(const float probability) {
  return BoundedFloatToValue(probability, kMinProbability, kMaxProbability);
}

// Converts a probability to a uint16 in the [1, 32767] range.
inline uint16 ProbabilityToValue(const float probability) {
  return BoundedFloatToValue(probability, kMinProbability, kMaxProbability);
}

整数区间value向浮点数映射：

extern const std::vector<float>* const kValueToProbability;
extern const std::vector<float>* const kValueToCorrespondenceCost;

// Converts a uint16 (which may or may not have the update marker set) to a
// probability in the range [kMinProbability, kMaxProbability].
inline float ValueToProbability(const uint16 value) {
  return (*kValueToProbability)[value];
}

// Converts a uint16 (which may or may not have the update marker set) to a
// correspondence cost in the range [kMinCorrespondenceCost,
// kMaxCorrespondenceCost].
inline float ValueToCorrespondenceCost(const uint16 value) {
  return (*kValueToCorrespondenceCost)[value];
}

Probability的Value转成CorrespondenceCost的Value:

inline uint16 ProbabilityValueToCorrespondenceCostValue(
    uint16 probability_value) {
  if (probability_value == kUnknownProbabilityValue) {
    return kUnknownCorrespondenceValue;
  }//如果是Unknown值还返回unknown值。Probability和CorrespondenceCost的Unknown值都是0
  bool update_carry = false;
  if (probability_value > kUpdateMarker) {//如果该值超过最大范围：但什么情况下会导致出现该值超过范围还不清楚
    probability_value -= kUpdateMarker;//防止溢出范围
    update_carry = true;//如果存在过超出范围的行为，则将update_carry置为true
  }
  //ProbabilityValue-->Probability-->CorrespondenceCost-->CorrespondenceCostValue
  uint16 result = CorrespondenceCostToValue(
      ProbabilityToCorrespondenceCost(ValueToProbability(probability_value)));
  if (update_carry) result += kUpdateMarker;//原先减去过一个最大范围，现在再加回来
  return result;
}

同样，CorrespondenceCost的Value也可以转成Probability的Value：

inline uint16 CorrespondenceCostValueToProbabilityValue(
    uint16 correspondence_cost_value) {
  if (correspondence_cost_value == kUnknownCorrespondenceValue)
    return kUnknownProbabilityValue;
  bool update_carry = false;
  if (correspondence_cost_value > kUpdateMarker) {
    correspondence_cost_value -= kUpdateMarker;
    update_carry = true;
  }
  uint16 result = ProbabilityToValue(CorrespondenceCostToProbability(
      ValueToCorrespondenceCost(correspondence_cost_value)));
  if (update_carry) result += kUpdateMarker;
  return result;
}

接下来几个函数在http://probability_values.cc中：

将一个uint16型的value转成一个浮点数。value的范围是[1,32767]，若value为0，表示是unknown。若是[1,32767]，则映射到浮点型的范围[lower_bound, upper_bound].

// 0 is unknown, [1, 32767] maps to [lower_bound, upper_bound].
//在计算时并不是用浮点数进行的计算，二是将0~1的概率值映射到1_32767的整数值
float SlowValueToBoundedFloat(const uint16 value, const uint16 unknown_value,
                              const float unknown_result,
                              const float lower_bound,
                              const float upper_bound) {
  CHECK_GE(value, 0);//是否大于等于0
  CHECK_LE(value, 32767);//是否小于等于0
  if (value == unknown_value) return unknown_result;
  const float kScale = (upper_bound - lower_bound) / 32766.f;
  return value * kScale + (lower_bound - kScale);
}

由： $\frac{value-1}{32766}=\frac{return-lower_{bound}}{upper_{bound}-lower_{bound}}$

得： $return=(value-1)\frac{upper_{bound}-lower_{bound}}{32766}+lower_{bound}$

把[1,32767]之间的所有value预先计算出来其映射到[lower_bound, upper_bound]这个区间的对应浮点值，存到一个浮点型向量中：

// 把[1,32767]之间的所有value预先计算出来其映射到[lower_bound, upper_bound]这个区间
// 的对应浮点值，存到一个浮点型向量中：
std::unique_ptr<std::vector<float>> PrecomputeValueToBoundedFloat(
    const uint16 unknown_value, const float unknown_result,
    const float lower_bound, const float upper_bound) {
  auto result = common::make_unique<std::vector<float>>();
  // Repeat two times, so that both values with and without the update marker
  // can be converted to a probability.
  for (int repeat = 0; repeat != 2; ++repeat) {
    for (int value = 0; value != 32768; ++value) {
      result->push_back(SlowValueToBoundedFloat(
          value, unknown_value, unknown_result, lower_bound, upper_bound));
    }
  }
  return result;
}

下面两个函数通过调用上面这个公式将Value值映射到Probability或CorrespondenceCost：

std::unique_ptr<std::vector<float>> PrecomputeValueToProbability() {
  return PrecomputeValueToBoundedFloat(kUnknownProbabilityValue,
                                       kMinProbability, kMinProbability,
                                       kMaxProbability);
}

std::unique_ptr<std::vector<float>> PrecomputeValueToCorrespondenceCost() {
  return PrecomputeValueToBoundedFloat(
      kUnknownCorrespondenceValue, kMaxCorrespondenceCost,
      kMinCorrespondenceCost, kMaxCorrespondenceCost);
}

然后，把预先计算出来的Probability和CorrespondenceCost放到在probability_values.h中定义的两个向量kValueToProbability和kValueToCorrespondenceCost中。这样，以后直接以value为索引值查表就可以获得其对应的probability或correspondenceCost。

const std::vector<float>* const kValueToProbability =
    PrecomputeValueToProbability().release();

const std::vector<float>* const kValueToCorrespondenceCost =
    PrecomputeValueToCorrespondenceCost().release();

接下来ComputeLookupTableToApplyOdds这个函数的功能比较难理解。我们这里做一个简单的解释。假设我们现在有一个cell，这里存着一个ProbabilityValue, 如果这时候我们通过传感器测量得到了一个新的观测结果 $odds_{z}$ ，那么我们应该如何更新这个cell的ProbabilityValue呢？还记得我们之前写的概率模型更新公式吗？

$odd(s|z)=\frac{p(z|s=1)}{p(z|s=0)}odd(s)$

如上所示，其中 $\frac{p(z|s=1)}{p(z|s=0)}$ 是我们的观测模型，根据我们观测到的是hit还是miss的情况，新的观测 $odds_{z}$ 只有两种情况：

$Hit:odds_{z}=\frac{p(z|s=1)}{p(z|s=0)}odds(s)$

或

$Miss:odds_{z}=\frac{p(z=0|s=1)}{p(z=0|s=0)}$

这两种情况的 $odds_{z}$ 值在传感器确定后是已知确定的。

那么，假设，我们某一个cell的ProbabilityValue是已知的,我们用 $p_{value}$ 表示，那么我们把这个值先转成概率值 $p$ ,然后再转成odds值。之后通过上面的公式：

$odd(s|z)=odds_{z}odd(s)$

就可以计算出更新后的odds值，然后再把该值转化成概率值，最后再把概率值转化为ProbabilityValue值。

上面这个流程就是ComputeLookupTableToApplyOdds函数所做的工作，所不同的是，该函数把 $value\sim[1,32767]$ 之间的所有value都预先计算出来，存成一个表，那么这样在使用时就可以以当前cell的value为索引值直接查找到更新后的结果value。那么 $odds_{z}$ 有两种不同的情况，所以我们存两个表就可以了。

在程序运行过程中，需要不停地更新，那么这样预先计算一次之后，以后就不用再计算，直接查表就可以，能节省大量的时间。不得不说，cartographer的这个设计是一个十分有才的设计。

// 该函数的含义是，对于一个value~[1,32767], 如果有一个新的odds值的观测后，更新后的value应该是什么。
// 这里对所有可能的value都进行了计算，存在了一个列表中。odds只有两种情况，hit或misses. 
// 因此，可以预先计算出来两个列表。这样，在有一个新的odds时可根据原有的value值查表得到一个新的value值，更新
std::vector<uint16> ComputeLookupTableToApplyOdds(const float odds) {
  std::vector<uint16> result;
  result.push_back(ProbabilityToValue(ProbabilityFromOdds(odds)) +
                   kUpdateMarker);//这个表示这个表中的第一个元素对应了如果之前该点是unknown状态，更新的value应该是什么
  for (int cell = 1; cell != 32768; ++cell) {
    result.push_back(ProbabilityToValue(ProbabilityFromOdds(
                         odds * Odds((*kValueToProbability)[cell]))) +
                     kUpdateMarker);
  }
  return result;
}

在ComputeLookupTableToApplyOdds，以及接下ComputeLookupTableToApplyCorrespondenceCostOdds，转化里都加了一个kUpdateMarker，相当于有了一个偏移。为什么要有这个偏移，这和同时可用于判断该栅格是否更新过有关，见后面的“三、概率更新查找表：hit_table_、miss_table_”。

同时，这个函数也在列表索引0处放置一个元素，这个元素对应着当当前cell是unknown情况下我们如何给该cell赋初值。这种情况下直接把 $odds_{z}$ 转成概率值，再转成ProbabilityValue就可以了。这样，所有情况都可以直接查表而得。

基于同样的原理，ComputeLookupTableToApplyCorrespondenceCostOdds是处理某一个cell的CorrespondenceCostValue已知时如何更新的情况：

std::vector<uint16> ComputeLookupTableToApplyCorrespondenceCostOdds(
    float odds) {
  std::vector<uint16> result;
  result.push_back(CorrespondenceCostToValue(ProbabilityToCorrespondenceCost(
                       ProbabilityFromOdds(odds))) +
                   kUpdateMarker);
  for (int cell = 1; cell != 32768; ++cell) {
    result.push_back(
        CorrespondenceCostToValue(
            ProbabilityToCorrespondenceCost(ProbabilityFromOdds(
                odds * Odds(CorrespondenceCostToProbability(
                           (*kValueToCorrespondenceCost)[cell]))))) +
        kUpdateMarker);
  }
  return result;
}

这里特殊说明一下，Grid2D里存的都是CorrespondenceCostValue

看完这部分代码我更加不理解论文原文中的公式(3)到底是什么意思了。根据代码来看，cartographer更新cell中概率值的方法跟我们在本文第一部分的推导是一致的。但是对于公式(3):

$M_{new}\left( x \right)=clamp(odds^{-1}(odds(M_{old}\left( x \right)).odds(p_{hit})))$

其中 $M\left( x \right)$ 到底存储的是什么呢？从代码来看，Grid2D中存的是CorrespondenceCost。按我的理解，应该是先将CorrespondenceCost转成Odds（我们暂时忽略CorrespondenceCost与CorrespondenceCostValue的相互转化），然后跟 $odds(p_{hit})$ 相乘，最后再转成CorrespondenceCost。但是这个公式中 $odds^{-1}$ 到底表示什么意思呢？如果表示取倒数，那对 $odds(M_{old}\left( x \right))$ 取倒数是什么意思呢？如果是表示 $odds(.)$ 的逆过程——即求一个odds值所对应的CorrespondenceCost是什么，那也应该是先让 $odds(M_{old}\left( x \right))$ 与 $odds(p_{hit})$ 相乘后再求 $odds^{-1}$ 啊。

所以，我合理地怀疑这个公式是不是存在typos呢？如果有读者比较清楚这里是怎么回事，烦请留言告知。

该文评论中“图图不吃兔兔”关于公式(3)理解：M(x)应该就是x这个cell所对应的probability value，是个1_32768的整数类型； odds()代表将probability value转换到odds值， odd^-1() 代表的就是将odds值转换到probability value值。根据代码也可以看出来，这里其实就是进行了浮点数到整数的映射，方便运算而已。

三、概率更新查找表：hit_table_、miss_table_

看cartographer是怎么使用上面介绍的理论。概率图中，两相邻坐标间的单元称为栅格，存储在栅格中的便是CorrespondenceCostValue，即表示该栅格是Free的概率，值范围[0~65535]。

更新概率图中各个栅格概率值时，采用以空间换时间的策略，主要是建立概率更新查找表，然后更新过程就直接变成了查表操作。牺牲内存空间，节约时间。其具体操作流程如下。

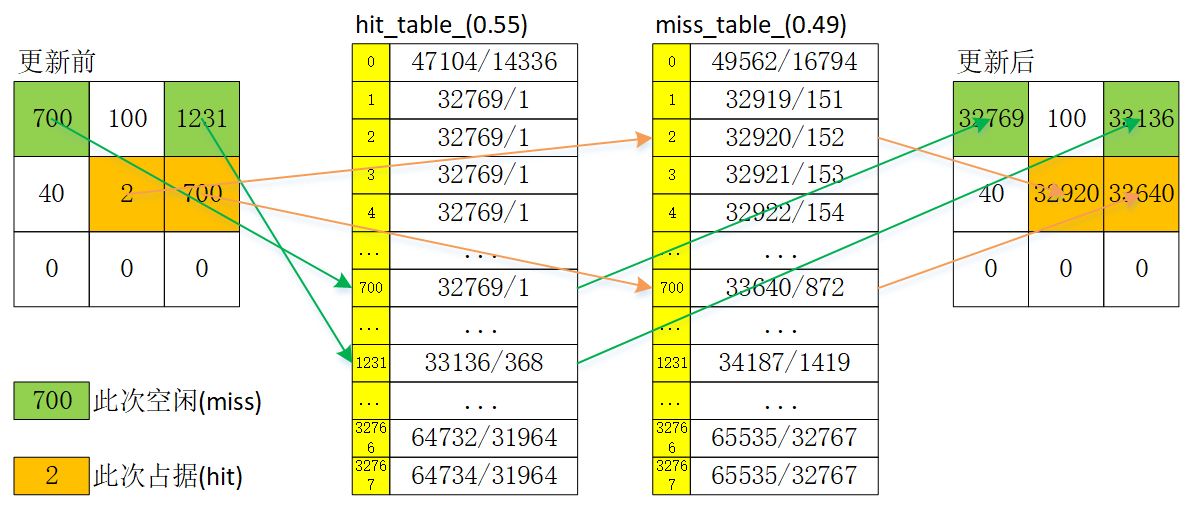
如图1所示，当(0,0)栅格中的值是700时，且此次是Occupied，通过查hit_table_表可立即获得更新后的值32769，然后直接填回该栅格，即可完成(0,0)栅格概率值更新。当(1,1)栅格中的值是2时，且此次是Free，通过查miss_table_表可立即获得更新后的值32920，然后直接填回该栅格，即可完成(1,1)栅格概率值更新。那本质上说，概率更新表存储着更新后的值，而表的索引就是更新前的值。至于构建表的方法是ComputeLookupTableToApplyCorrespondenceCostOdds。

代码中构建这两张表的入口在ProbabilityGridRangeDataInserter2D构造函数。

ProbabilityGridRangeDataInserter2D::ProbabilityGridRangeDataInserter2D(
    const proto::ProbabilityGridRangeDataInserterOptions2D& options)
    : options_(options),
      hit_table_(ComputeLookupTableToApplyCorrespondenceCostOdds(
          Odds(options.hit_probability()))),
      miss_table_(ComputeLookupTableToApplyCorrespondenceCostOdds(
          Odds(options.miss_probability()))) {}

ComputeLookupTableToApplyCorrespondenceCostOdds需要一个表示传感器特性的odds参数，图1中构建hit_table_是Odds(0.55)，miss_table_则是Odds(0.49)。它们分别来自lua配置中的hit_probability、miss_probability。

hit_probability = 0.55。含义是在实际状态为occupied的条件下，测量结果是“occupied”的概率。以更新前是unknown(0)解释下过程。点云报告此栅格是占据(occupied)，根据Probablity=0.55算出CorrespondenceCost是0.45，由CorrespondenceCost算出CorrespondenceCostValue是14336。正是图1中hit_table_[0]的值。
miss_probability = 0.49。含义是在实际状态为free的条件下，测量结果是“occupied”的概率。以更新前是unknown(0)解释下过程。点云报告此栅格是空闲(free)，根据Probablity=0.49算出CorrespondenceCost是0.51，由CorrespondenceCost算出CorrespondenceCostValue是16794。正是图1中miss_table_[0]的值。

通过看图1中的hit_table_、miss_table_值，还可归纳这表的几个特点。

两个表的长度都是32768。
表索引0表示之前是kUnknownCorrespondenceValue(0)时，此次hit或miss，更新后是什么值。
表中所有值都一定>=32768(kUpdateMarker)，包括索引0。

这里kUpdateMarker为已更新后的标志量，是为了防止miss和hit重复更新某个栅格，其值为32768，为uint16的最高位。以下是操作逻辑。

[ApplyLookupTable]更新cell-A时会自动得到一个>=kUpdateMarker的值，并把cell-A坐标放入update_indices_集合。
[ApplyLookupTable]如果此帧点云又判断出要更新cell-A，但发现值已>=kUpdateMarker，认为此轮已更新过，不执行操作。
[Grid2D::FinishUpdate]更新完了此帧点云，将update_indices_集合中的栅格值减去kUpdateMarker。

正是以上这个过程，要求kValueToCorrespondenceCost[idx]和kValueToCorrespondenceCost[idx + kUpdateMarker]有着同样值。因为这，从0到32767，PrecomputeValueToBoundedFloat重复计算了2次。[0, 32767]、[32768, 65535]区别了带kUpdateMarker和不带kUpdateMarker，但都可以获得相同的概率值。

有关概率更新过程，网上另一篇文章：【图解 cartographer】之地图概率更新过程

参考

Cartographer源码阅读之附 1—probability_values.h/c：占据概率相关 https://zhuanlan.zhihu.com/p/49030629

probability_values.h/c：占据概率相关

参考

全部评论: 0 条